
Longitude by Sextant: The Sun’s Equal-Altitudes Method at sea : explanation and two fully worked-out examples.

Introduction
If the Sun culminates high enough in the sky, it is possible to determine one’s position by taking three observations: just before, at the moment of, and just after its upper meridian passage.

This procedure relies on two distinct steps.
The first method consists in measuring two equal altitudes of the Sun, one before and one after its meridian passage, each recorded with the exact time of observation.
These observations, called equal altitudes — or corresponding circumzenithal altitudes — make it possible to determine the exact time of upper meridian passage and therefore deduce the longitude with the help of the nautical almanac.
The second consists of observing the Sun at its meridian culmination, in order to obtain the latitude using the classical method already presented on the local apparent noon sight latitude
One might wonder why the exact time at the moment of the Sun’s culmination is not used.
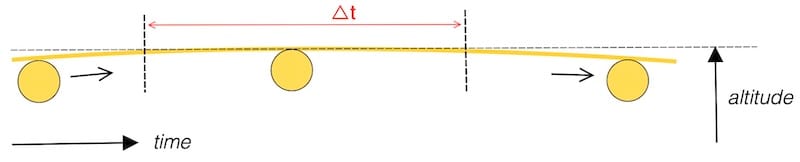
The figure shows that measuring the maximum altitude is not difficult, but that determining the exact instant of culmination is impossible within the Δt interval: the change in altitude is too small to allow reliable time determination.

Returning to the first step: when measuring two identical altitudes of the Sun—one before and one after its meridian passage—in conditions of reduced visibility (haze, swell, an indistinct horizon), it is advisable to take multiple series of sights.
This increases the likelihood of obtaining matching altitude pairs and improves the accuracy of the averaging of the observation times.

Practical advantages and limitations
Although this method is mostly used in the tropics, where the Sun generally culminates high enough — ideally at altitudes of 78° or more — it can also be applied at mid-latitudes, provided the Sun reaches at least 60° of altitude.
The equal-altitude method is accurate only when the Sun’s path is sufficiently symmetrical around meridian passage, which requires a high meridian altitude and observations taken close to Local Apparent Noon. At high culminations the altitude changes quickly, giving a clear observation time; at lower culminations it changes slowly, making timing uncertain. The method is therefore most reliable in tropical latitudes.
Fundamentals of the equal-altitude method
The principle of the equal-altitudes method is extremely simple.
Because the two observations are made at the same apparent altitude—one before and one after the Sun’s upper meridian passage—the instrumental errors of the sextant cancel out. For the purpose of determining the time of equal altitudes, no correction for the instrument’s intrinsic error is therefore required.
In this method, the altitude itself is used only for comparison: the essential element lies in the exact timing of the two observations.
However, when computing the meridian altitude in order to determine the local apparent noon (LAN) latitude, all standard corrections must of course be applied, including index error, dip, refraction, and the Sun’s semi-diameter.
On the other hand, the method provides with remarkable precision the time of meridian (LAN) passage, which makes it an excellent way to check the chronometer (or wristwatch). At that same moment, it also offers the possibility — in a very straightforward way — of determining longitude using the nautical almanac.

Although simple and theoretically precise, the equal-altitudes method remains time-consuming to carry out and requires experience. One must master both taking observations and controlling the observation timing, while also accounting for the vessel’s movement, because the vessel’s movement introduces additional corrections.
Thus, it remains an excellent educational tool for learning celestial navigation, rather than a truly practical operational method at sea.
But in calm seas and clear skies, the exercise can be very satisfying… and the captain’s cocktail will just have to wait!

Conduct of the observations
The observer measures two equal altitudes of the Sun:
One before local apparent noon (LAN).
The other after local apparent noon.
Since these two altitudes are identical, the Sun is symmetrically positioned with respect to the observer’s meridian. The midpoint in time between the two observation times therefore corresponds to local apparent noon. For now, we assume that the vessel’s position has not changed between the two observations.

Note on LAN Latitude
Observing when the Sun reaches its greatest altitude between T1 and T2 makes it possible to calculate the LAN latitude. This method does not rely on the equal-altitudes method.
LAN Longitude
At the moment (T1 + T2) / 2, expressed in UT, the observer is at local apparent noon; the Sun’s Greenwich hour angle at that instant therefore gives the vessel’s longitude.
The first GHA tables were published in 1767 by the British Nautical Almanac.
Reminder: hour angles run from 0° to 360° westward.
However, for geographical coordinates on Earth, we use:
– East longitude: 0° to 180°
– West longitude: 0° to 180°
Thus, the longitude can be determined as follows:
If GHA < 180° ⇒
West longitude = GHA.
If GHA > 180° ⇒
East longitude = 360° − GHA.

In practice
In practice, one does not limit the process to just two observations. Several altitudes of the Sun are taken before and after its meridian passage — typically three to six measurements on each side — in order to obtain multiple pairs of equal altitudes.
Each pair provides a specific instant at which the two altitudes are equal. By averaging these instants, one obtains the time of local apparent noon with greater precision.
Rate of Observation Before Culmination (Equal Altitudes Method)
The table below provides practical guidance on the useful duration of observations, based on the estimated altitude of the Sun at the moment of its culmination.


Observations
| Hs | UT ( h m s) | |
| before T1 | ||
| before T2 | ||
| before T3 | ||
| LAN | ———– | |
| after T4 | ||
| after T5 | ||
| after T6 |

This guidance, taken from the authoritative French book Traité de navigation, assumes that typically three to six measurements before and after culmination are carried out.
It is then sufficient to read the Sun’s GHA in the almanac corresponding to this average UT time. This value directly gives the vessel’s longitude.
Why apply a correction for the vessel’s movement?
Movements that are not purely east⎼west disturb the symmetry of the equal altitudes, because they produce a change in the vessel’s latitude and, consequently, in the apparent altitude of the Sun. The magnitude of the correction caused by north⎼south movement depends on the difference between latitude and declination and becomes increasingly significant as the vessel’s speed increases.”
Formula for the correction to apply (Δλ) — result in minutes of arc:
Δλ = 12/π × SOG × cos COG × (tanD − tanL)
where:
– SOG= vessel’s speed over the ground (in knots)
– COG= course over the ground
– L = vessel’s latitude
– D = Sun’s declination
The correction is zero
The correction becomes zero when:
– the vessel is stationary (SOG = 0),
– the course is east⎼west (cos COG = 0),
– the latitude equals the declination (tan D – tan L = 0).
Conclusion on the sign of the correction Δλ
The sign of the correction Δλ depends entirely on the vessel’s direction of movement and on the relative position of the Sun with respect to the ship’s latitude.
Thus, the sign of Δλ is determined by the product, which may be positive or negative.
We then apply the formula: Corrected GHA = GHA − Δλ.
Always subtract Δλ from GHA, keeping its algebraic sign.
This expression is valid in all cases, with no distinction of hemisphere or season, provided the actual algebraic sign of Δλ given by the formula is preserved.
To simplify the use of this rather heavy formula, a table is provided. It gives the same result, although with slightly lower accuracy due to rounding. This downloadable table is accompanied by six examples.
Additional explanation
Moving toward the Sun (the Sun’s altitude increasing)
→ the vessel is moving toward the Sun’s declination
→ local true noon occurs earlier
→ with the Sun’s hour angle decreasing
Moving away from the Sun (the Sun’s altitude decreasing)
→ the vessel is moving away from the Sun’s declination
→ local true noon occurs later
→ with the Sun’s hour angle increasing

Example 1: Meridian latitude and—independently—longitude by the method of equal altitudes of the Sun.
On 19 August 2025 at 01:00 UT (T1), the estimated position is:
06° 33.7′ N
129° 36.6′ E
COG = 210°
SOG = 10 knots
We can calculate the zone time (ZT), or the local time on board, from the chosen UT.
Longitude = 129° 36.3′ East (between 127.5° and 142.5°)
ZD = − 9
ZT = UT – ZD = 01h 00 − (− 9) = 10 h 00
Calculate the latitude and longitude at the moment of the LAN passage.
Preparation before the observations
- Calculation of the approximate LAN time:
- Calculation of the approximate altitude at the moment of LAN passage:
- Use of the table “Rate of Observation Before Culmination (Equal Altitudes Method)” with the previously calculated approximate time and altitude.
Observations
4.
| Hs | UT ( h m s) | |
| before T1 | ||
| before T2 | ||
| before T3 | ||
| LAN time | ||
| after T4 | ||
| after T5 | ||
| after T6 |
Final calculation
- Calculation of the LAN latitude:
- Calculation of the exact LAN time:
- Calculation of the longitude at the moment of LAN passage:
1) Calculation of the approximate LAN time
We begin by calculating the approximate LAN time, as explained on the page: Local Apparent Noon Time at sea
19 August 2025 (Nautical Almanac)
| UT | GHA☉ | Declination |
|---|---|---|
| 00 | 179° 04.6’ | 12° 45.3’ N |
| 01 | 194° 04.8’ | 12° 44.5’ N |
| 02 | 209° 04.9’ | 12° 43.7’ N |
Calculation: LHA = GHA + G (East)
| GHA = 194° 04.8’ | 01 h 00 UT (T1) |
| G = 129° 36.6’ E | |
| ______________ + | |
| LHA = 323° 41.4’ | |
| P = 36° 18.6’ |
The calculation of the polar angle (P) is central to the core exercise on easysextant.com.

△t = P ÷ 15
△t = 36° 18.6’ ÷ 15 = 2 h 25 m 14 s
The approximate LAN time:
T1 + △t = 01 h 00 + 2 h 25 = 03 h 25 UT
2) Calculation of the approximate altitude at meridian passage
h = 90° − |L − D|
|L − D|: This is simply the difference between the estimated latitude (L) and the Sun’s declination (D), taken as an absolute value.
Latitude (L) at 03 h 25 UT ≈ 6° 10’ N (dead reckoning taken from the chart)
Declination (D) at 03 h 25 UT ≈ 12° 42.5’ N
19 August 2025 (Nautical Almanac):
| UT | GHA☉ | Dec |
|---|---|---|
| 03 | 224° 05.1’ | 12° 42.9’ N |
| 04 | 239° 05.2’ | 12° 42.0’ N |
|L − D| = | 6° 10’ N − 12° 42.5’ N |
=∣ − 6° 32.5′ ∣ which gives 6° 32.5′ (absolute value)
Approximate altitude at LAN passage:
h = 90° − |L − D| = 90° − 6° 32.5′ = 83° 27.5′
3) Use of the table: Observation rate before and after culmination. (Equal-Altitudes Method)


Therefore, according to the table, the observations should begin approximately 9⎼10 minutes before, and end 5⎼6 minutes before the meridian passage. The use of this table does not require absolute precision, but it provides a useful guideline.
The observations.
(UT = Universal Time)
| Hs | UT ( h m s) | |
| before T1 | 82° 49.3’ | 03 15 11 |
| before T2 | 82° 52.3’ | 03 15 43 |
| before T3 | 82° 55.3’ | 03 16 18 |
| LAN altitude (Hs) | 83°19.2’ | ≈ 03 26 |
| after T4 | 82° 55.3’ | 03 35 17 |
| after T5 | 82° 52.3’ | 03 35 53 |
| after T6 | 82° 49.3’ | 03 36 28 |
5) Calculation of the LAN latitude
Once the table has been completed, we put the sextant away and start computing the LAN latitude.

The declination (D), obtained from the daily pages in the nautical almanac, is positive in the Northern Hemisphere and negative in the Southern Hemisphere.
The zenith distance (α) is taken as positive when the Sun is observed to the south at the time of LAN, and negative when the Sun is observed to the north.
Hs = 83° 19.2’ at LAN
Index error ℇ = ⎼2.2’
Eye height = 4 m


| Hs | 83° 19.2’ |
| ℇ | ⎼ 2.2’ |
| dip | ⎼ 3.5’ |
| + ________ | |
| Ha | 83° 13.5’ |
| altitude corr. table | 15.8’ |
| Sun’s lower limb correction LL | |
| + _________ | |
| Ho | 83° 29.3’ |
𝛂 = 90° − Ho = 90° − 83° 29.3’ = 06° 30.7’
𝛂 = −06°30.7′ (Sun to the north)
LAN latitude = D + 𝜶
12° 42.5’ + ( −06° 30.7’) = 06° 11.8’ N
6) Calculation of the exact LAN time
Each pair of equal altitudes provides a time interval symmetrically distributed around local apparent noon. The midpoint in time between the two corresponding observations therefore represents an estimate of the LAN time.
When several equal-altitude pairs are available, the exact LAN time is obtained by averaging the observation times of all sights taken before and after culmination. This averaging reduces random observation errors and improves the precision of the result.
(T1 + T2 + T3 + T4 + T5 + T6) / 6
= 03 h 25 m 48 s (in UT)
Thus, the exact LAN time is obtained and is required to determine the longitude.
7) Calculation of longitude at LAN
From this average time, we obtain the Sun’s GHA from the nautical almanac. This value directly gives the ship’s longitude, to which we must however add the correction for the vessel’s movement.
19 August 2025 (the nautical almanac)
| UT | GHA | D |
| 03 | 224°05.1’ | 12°42.9’ N |
| 04 | 239°05.2 | 12°42.0’ N |
| UT | GHA |
| 03 00 00 | 224° 05.1’ |
| * increment 00 25 48 + | 6° 27’ + |
| 03 25 48 | 230° 32.1’ |
* 00 h 25 m 48 s × 15° = 6° 27′
GHA = 230°32.1’
If the vessel’s speed has been zero, then GHA = 230°32.1’, which is the GHA at LAN time.

However, we must add the correction for the vessel’s movement.
Δλ = 12/π × SOG × cos COG × (tanD − tanL)
Δλ = (12/π) × 10 × cos 210° × ((tan 12°42.5’) − (tan 6°11.7’))
⇒ Δλ = ⎼ 3.9’
Corrected GHA = GHA − Δλ’
= 230°32.1’ − (−3.9)’ = 230°36.0’
If GHA < 180° ⇒ Longitude West = GHA.
If GHA > 180° ⇒ Longitude East = 360° − GHA.
GHA > 180° ⇒ 360° − 230° 36.0′ = 129° 24.0′
Longitude(G) at LAN time:
G LAN = 129°24.0‘ E
Example 2: Meridian latitude and—independently—longitude by the method of equal altitudes of the Sun.
On 14 December 2025 at 21:00 UT (T1), the estimated position is:
38° 37.6′ S
160° 32.5′ W
COG = 040°
SOG = 11 knots
We can calculate the zone time (ZT), or the local time on board, from the chosen UT.
Longitude = 160° 32.5 W (between 157.5° and 172.5°)
ZD = + 11
ZT = UT – ZD = 21h 00 − (+ 11) = 10 h 00
Calculate the latitude and longitude at the moment of the LAN passage.
1) Calculation of the approximate LAN time
We begin by calculating the approximate LAN time, as explained on the page: Local Apparent Noon Time at sea
14 December 2025 (Nautical Almanac)
| UT | GHA☉ | Declination |
|---|---|---|
| 21 | 136° 16.0’ | 23° 15.6’ S |
| 22 | 151° 15.7’ | 23° 15.7’ S |
| 23 | 166° 15.4’ | 23° 15.9’ S |
Calculation: LHA = GHA − G (West)
| GHA = 136° 16.0’ | 21 h 00 UT (T1) |
| G = 160° 32.5′ W | |
| ______________ ⎼ | |
| LHA = 335° 43.5’ | |
| P = 24° 16.5’ |
The calculation of the polar angle (P) is central to the core exercise on easysextant.com.

△t = P / 15
△t = 24° 16.5’ / 15 = 1 h 37 m
The approximate LAN time:
T1 + △t = 21 h 00 + 1 h 37 = 22 h 37 UT
⇒ 11 h 37 ZT
2) Calculation of the approximate altitude at meridian passage
h = 90° − |L − D|
|L − D|: This is simply the difference between the estimated latitude (L) and the Sun’s declination (D), taken as an absolute value.

Latitude (L) at 22 h 37 UT ≈ 38° 24′ S (dead reckoning taken from the chart)
Declination (D) at 22 h 37 UT ≈ 23° 16’ S
|L − D| =| ⎼ 38° 24’ − ( −23° 16′) |
=∣ − 15° 08′ ∣ which gives 15° 08 ′ (absolute value)
Approximate altitude at LAN passage:
h = 90° − |L − D| = 90° − 15° 08′ = 74° 52′
3) Use of the table: Observation rate before and after culmination. (Equal-Altitudes Method)

According to the table, the observations should begin approximately 10⎼12 minutes before, and end 6⎼9 minutes before the meridian passage. The use of this table does not require absolute precision, but it provides a useful guideline.
The observations.
(UT = Universal Time)
| Hs | UT ( h m s) | |
| before T1 | 74° 20.9′ | 22 23 44 |
| before T2 | 74°22.9’ | 22 24 32 |
| before T3 | 74° 24.9’ | 22 25 30 |
| LAN altitude (Hs) | 74°36.8’ | ≈ 22 37 |
| after T4 | 74° 24.9’ | 22 48 18 |
| after T5 | 74°22.9’ | 22 49 13 |
| after T6 | 74° 20.9′ | 22 50 07 |
5) Calculation of the LAN latitude
Once the table has been completed, we put the sextant away and start computing the LAN latitude.

The declination (D), obtained from the daily pages in the nautical almanac, is positive in the Northern Hemisphere and negative in the Southern Hemisphere. Here 23°15.8 S from nautical almanac.
The zenith distance (α) is taken as positive when the Sun is observed to the south at the time of LAN, and negative when the Sun is observed to the north.
Hs =74° 36.8’ at LAN
Index error ℇ = 2’
Eye height = 3 m


| Hs | 74° 36.8’ |
| ℇ | 2’ |
| dip | ⎼ 3’ |
| + ________ | |
| Ha | 74° 35.8’ |
| altitude corr. table | 15.9’ |
| Sun’s lower limb correction LL | |
| + _________ | |
| Ho | 74° 51.7′ |
𝛂 = 90° − Ho = 90° − 74° 51.7’ = 15° 08.3’
𝛂 = −15°08.3′ (Sun to the north)
LAN latitude = D + 𝜶
⎼23° 15.8’ + ( −15° 08.3) = 38° 24.1’ S
6) Calculation of the exact LAN time
Each pair of equal altitudes provides a time interval symmetrically distributed around local apparent noon. The midpoint in time between the two corresponding observations therefore represents an estimate of the LAN time.
When several equal-altitude pairs are available, the exact LAN time is obtained by averaging the observation times of all sights taken before and after culmination. This averaging reduces random observation errors and improves the precision of the result.
(T1 + T2 + T3 + T4 + T5 + T6) / 6
= 22 h 36 m 54s (in UT)
Thus, the exact LAN time is obtained and is required to determine the longitude.
7) Calculation of longitude by LAN
From this average time, we obtain the Sun’s GHA from the nautical almanac. This value directly gives the ship’s longitude, to which we must however add the correction for the vessel’s movement.
14 December 2025
| UT | GHA | D |
| 21 00 00 | 136° 16.0′ | S 23° 15.6′ |
| 22 00 00 | 151° 15.7′ | S 23° 15.7′ |
| 23 00 00 | 166° 15.4′ | S 23° 15.9′ |
| UT | GHA |
| 22 00 00 | 151°15.7’ |
| * increment 00 36 54 + | 9°13.5’ |
| 22 36 54 | 160°29.2’ |
* 00 h 36 m 54 s × 15° = 9° 13.5′
GHA = 160°29.2’
If the vessel’s speed has been zero, then GHA = 160°29.2, which is the GHA at LAN time.

However, we must add the correction for the vessel’s movement.
Δλ = 12/π × SOG × cos COG × (tanD − tanL)
Δλ = (12/π) × 11 × cos 040° × ((tan ⎼23°15.8’) − (tan −38°24.1))
⇒ Δλ = 11.7’
Corrected GHA = GHA − Δλ’
= 160°29.2’ − (11.7)’ = 160°17.5’
If GHA < 180° ⇒ Longitude West = GHA.
If GHA > 180° ⇒ Longitude East = 360° − GHA.
Since GHA < 180° : G = GHA
Longitude(G) at LAN time:
G LAN = 160° 17.5‘ W