Local Apparent Noon Time (LAN) at sea: calculating the LAN time can be done very simply if we do not take the ship’s own movement into account.

First, review the theory of the noon sight
Not having the exact LAN time is not a problem. Indeed, it is sufficient to go outside 10 minutes beforehand and start taking observations of the sun at short intervals until the sun reaches its highest point and begins to descend. Note the altitude at the time of the highest point as well as the LAN time, without needing precision to the exact second.
To obtain a more precise meridian time, it is necessary to take the ship’s own movement into account. This can be important for fast ships that are heading more towards the east or west, but it complicates the calculation due to the formulas that need to be remembered.
Local Apparent Noon Time at sea: explanation:
Apparent Solar Time: This varies due to the Earth’s elliptical orbit and axial tilt, causing the sun’s apparent motion to speed up or slow down relative to the mean solar time.

Mean Solar Time: This is the average solar time over the year, assuming a uniform 24-hour day. (“Clock time” is our average, consistent time).

Equation of Time: The Equation of Time graph typically shows the difference (in minutes) between apparent solar time, as measured by a sundial, and mean solar time, as indicated by a watch, throughout the year. This difference oscillates, reaching up to about ±16 minutes.

This classic equation of time theory is good to know for a mariner, but we don’t have sundials on board. Additionally, every observer at a different longitude experiences a different apparent noon. Therefore, we need to apply an additional longitude correction to obtain the local apparent noon time.
Moreover, while navigating within the same time zone over the course of a year, apparent noon can occur as early as 11:19 or as late as 12:43, depending on the time of year and the difference in longitude. This variation doesn’t even take daylight saving time into account.

Local Apparent Noon Time at sea:
There are different techniques for calculating the noon time, and we will use the technique involving the polar angle. To calculate the noon time using this method, you need to know how to determine the polar angle (P) beforehand.
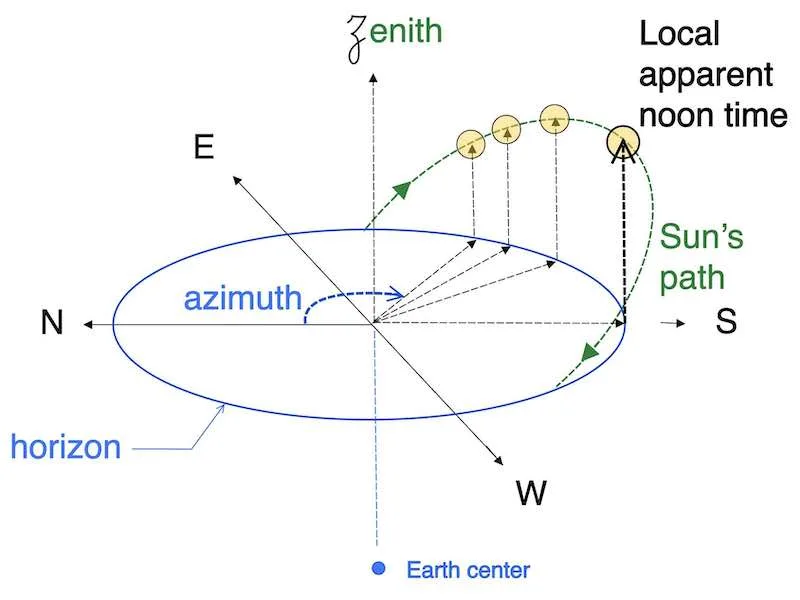
Remember, the main purpose of this website is to determine the sun’s Line of Position (LOP) at any time of the day using the Marcq St. Hilaire method, with the ‘La Rochelle’ exercise.
It is essential to understand that the local apparent sight technique as explained on this page can only be applied at a specific time of the day
Also, with the apparent noon time, the observer’s latitude, and the declination of the sun, you can plan the appropriate intervals between two or more sun sights for that day.

Initiating the local apparent noon (LAN) time , without the vessel’s own movement
As I have advocated in my course, we start the ocean passage with the downloaded daily pages from the nautical almanac.
Also we have a reliable watch set to UT time. !!

Early in the morning, for example after breakfast, we take the UT time of the next whole hour (T1) and the estimated longitude.
It’s better to use a whole hour (T1) so that we don’t have to calculate the increment from the minutes and seconds.
Remember to calculate the noon time, you need to know how to determine the polar angle (P) in advance!

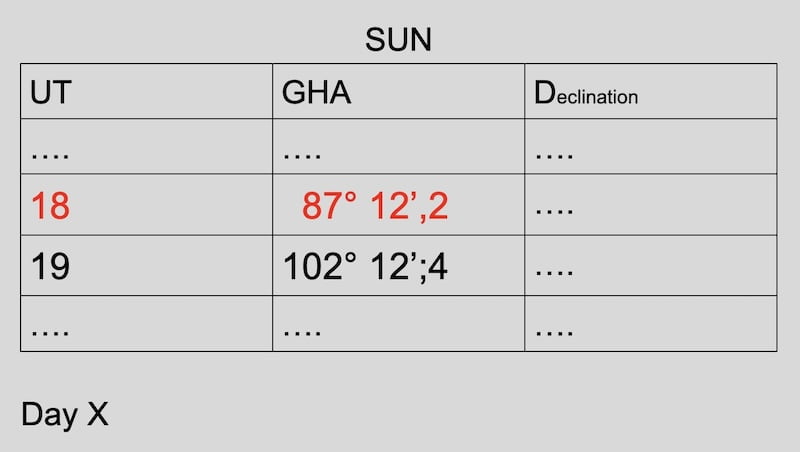
With this UT time (T1), we will look for the GHA in the nautical almanac and calculate P (polar angle)


let’s see how it works:
T1 = UT time whole hour = 18.00 hours
Day 26 January
L = 33°21’ N; G = 150°18’W
18.00 UT, corresponding to 08.00 local time (LT) on board.
150°18′ W is between 142,5° and 157,5 → time zone number = + 10

LT = UT ⎼ (Time zone number) = 18.00 ⎼ (+10) = 08.00 (time on board)

P will decrease to zero at a rate of 15° per hour, reaching zero at local apparent noon time.

18.00.00 + 04.12.00 = 22.12.00 UT Time
T local apparent noon (lan) = UT ⎼ ( + 10) = 12h 12m LT. (local time)
Astronomical Navigation: Calculating Local Noon time
EXERCISE
The movement of the ship is not taken into account.
Indeed, you are sailing off the coast of the Guadeloupe Islands on a beautiful, almost cloudless day. Your estimated position (D.R.) is 15°54.4′ N, 056°34′ W at 09:00 local time on board on June 6, 2022:
1.Calculate UT Time
2.Calculate the local noon.
3.Should I face the sun in the north or south direction at that time?
1.
UT = LT + Time Zone number
UT = 09.00 + ( +4) = 13.00
2.
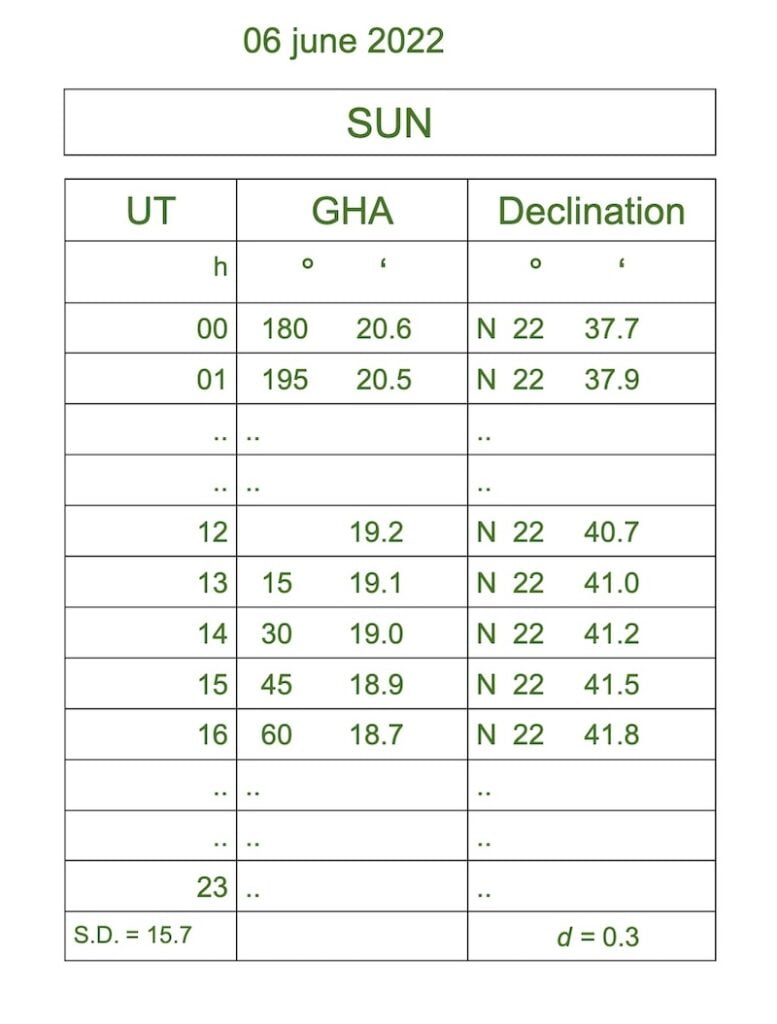
GHA = 15°19,1′ à 13h00 (T1)
G = 56°34,0′ W
________________ ⎼
LHA = 318°45,1′ ⇒ P = 41°14,9′
△t = P/15°
△t = 41,9° / 15° = 2h 45m
LAN Time = T1 + △t
LAN Time = 09h00 + 2h45 = 11h45
Le soleil est-il au nord ou au sud ?
Latitude = 15°54,4′ N Declination = 22°41′ N
D > L (hémisphère nord)
soleil North or South in the tropic
We are facing the sun in the northern direction.

In conclusion
Typically, during a noonsight, the observer measures the altitude of the sun when it is at its highest point in the sky (culmination). The altitude of the sun at this moment is directly related to the observer’s latitude.
By focusing on accurately measuring the sun’s altitude at its highest point, you eliminate the necessity for precise timekeeping during the observation, thereby saving time and simplifying the process. In other words, you do not need to record the time at that very moment; it’s just you, the sun, and the sextant.
However, it’s crucial to have a reliable and accurate sextant for measuring the sun’s altitude, as this measurement is key to determining your latitude.
ANNEX
Influences of Vessel Motion on lan determination:
The precision of determining local apparent noon (LAN) using this method is compromised by the influence of a vessel’s own motion, especially when navigating on a course close to east or west at high speed
As a matter of fact, this movement affects the time interval between T1 and local apparent noon.
Certainly, for individuals taking a noon sight, it is better to take into consideration the influence of the vessel’s own motion.

Local Apparent Noon Time at sea:
The exact method of how to calculate the local apparent noon:
Also, here we expose the exact local apparent noon calculation .
The uncertainty of the vessel’s speed and course can still affect the accuracy of this method.
Day X
Additionally, T1 is the UT time at the whole hour, which in our case is 18:00:00, corresponding to 08:00:00 local time, which is early in the morning on board of our vessel.
Remember, you can take any time as T1 before apparent noon; the final answer will be the same.
estimated position at 18:00:00 UT:
L = 33°21’ N;
G = 150°18’W
SOG (speed over ground) = 12 knots.
COG (course over ground) = 300°
GHA = 87°12’,2 at 18.00.00 UT


We have previously established that the accuracy of determining Local Apparent Noon (lan) is hindered by the impact of a vessel’s motion, particularly when navigating on a course close to east or west.
In fact, this movement alters the time interval between T1 and Local Apparent Noon.
Instead of using the sun’s rate of 15°, we adopt a relative rate that incorporates the vessel’s motion, as indicated by the formula below.


T lan = 12h 15m 56s local time
Finally, the difference between the method that takes into account the vessel’s own movement and the one that does not is about 4 minutes.
But if you are prepared 10 minutes before noon with your sextant outside and start following the sun’s ascension until its culmination, you will be able to find your latitude safely.

Local Apparent Noon Time at sea: Exercise
In fact, you are sailing offshore the Guadeloupian islands on a beautiful day with almost no clouds.
Your Dead Reckoning (D.R.) position is 15°54.4′ N, 056°34′ W.
At 09:00 local time on board 6 June 2022
1)Calculate the local apparent noon time
2)Do I face the sun in the northern or southern direction at this moment?
Also, assume the vessel’s movement is not taken into account.
Firstly, we have to calculate the UT
UT time = LT time + Time zone number
UT time = 09.00 + (+ 4) = 13.00

GHA = 15° 19’,1 (T1 = 13.00 UT)
G = 56° 34’0 W
————————— ⎼
LHA = 318° 45’,1
⇒ P = 41° 14’,9
△t = P/15°
⇔ △t = 41’,9 / 15° = 2h 45m
local apparent noon time = T1 + △t
⇔ local apparent noon time = 09h00 +2h45 = 11h45
Sun in the north or south?
Latitude = 15° 54’,4 N
Declination = 22° 41’ N
D > L (hemisphere North)
We will face the sun in the North
Now we do the same exercise but take the vessel’s movement into account.
COG (course over ground) = 065°
SOG (speed over ground = 8 knots

In conclusion, the method that accounts for the vessel’s movement differs from the one that does not by approximately one and a half minutes.
However, if you begin following the sun’s ascension ten minutes before the culmination point, this discrepancy is inconsequential.
