Sun’s altitude and azimuth calculation using a scientific calculator
Hc = Sun’s calculated altitude = sun’s calculated height
Zv = Sun’s true azimuth
The St. Marcq Hilaire method involves comparing two entirely different methods:
- Using the sextant to measure the height of the sun and, after some corrections, finding the observed altitude (Ho).
- Calculating, from our estimated position, the appropriate sun’s altitude (Hc)
On this page, we focus on the latter method.

Overall, please consider that the website’s overarching context commences with the La Rochelle exercise, leading you to an interactive worksheet.
Furthermore, The primary goal is to acquire the skill of determining your line of position at sea through a series of eight identical exercises.

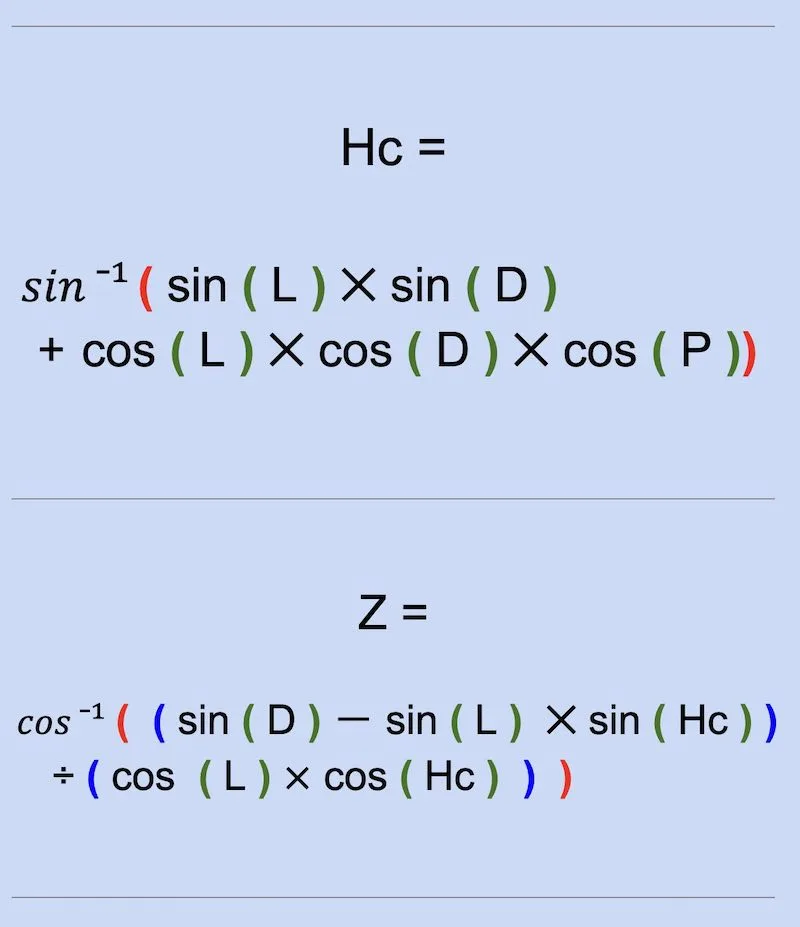
P = NW or SW ⟹Sun in the West ⟹ Zv = 360°- Z
Remember, You need to calculate the sun’s height Hc first before proceeding with the azimuth calculation Zv
In summary, the first exercise has been fully explained, and for the second exercise, you will need to complete it on your own.
To access the explanation and answer for the second exercise, click the provided hyperlink.


sun’s altitude and azimut calculation: First exercise for calculation Hc/zv
exercise for calculated height and true azimuth
calculated height
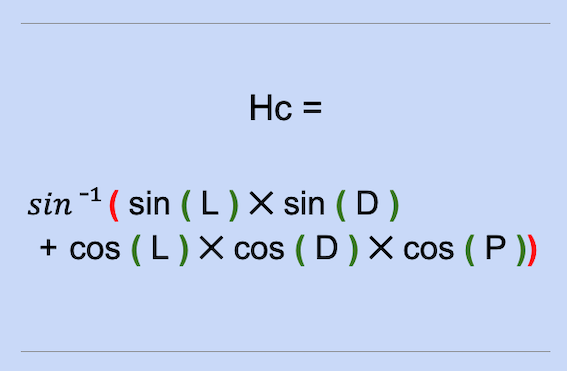
P is always positive in these formulas.
L and D positive if North
L and D negative if South
The entries obtained in the first part on our worksheet:
Estimated latitude (L)= 31° 29‘, 5 N
Declination (D) of the sun = 23 ° 18 ‘, 0 N
Polar angle (P) = 32 ° 23 ‘, 8 NE
P = NE: The Northern Hemisphere and the sun is in the East which means the sun is still rising. (Attention: Do not confuse with East longitude.)
Hc =
𝑠𝑖𝑛 ¯¹ (𝑠𝑖𝑛(31°29′,5)
✕ sin(23°18′)
➕ cos(31°29′,5)
✕ 𝑐𝑜𝑠(23°18′)
✕ 𝑐𝑜𝑠(32°23′,8))
Hc = 60 ° 13 ‘, 0

Ater finding Hc, we are going to calculate Zv.

sun’s altitude and azimut calculation:
True azimuth Zv

-L = 31° 29‘, 5 N
-D = 23 ° 18 ‘, 0 N
-Hc = 60 ° 13 ‘, 0
cos ¯¹ ( ( sin (23 ° 18 ‘, 0)
ー sin ( 31° 29‘, 5)
✕ sin (60 ° 13 ‘, 0) )
➗( cos (31° 29‘, 5)
✕ cos (60 ° 13 ‘, 0) ) )
Z = 97,8°
P = NE or SE ⟹Sun in the East ⟹ Zv = Z
P = NW or SW ⟹Sun in the West ⟹ Zv = 360°- Z
P = 32 ° 23 ‘, 8 NE ⟹ Zv = Z
Zv = 97,8° ⟹ 98°


sun’s altitude and azimut calculation: second exercise for calculation Hc/Zv
You need to complete it on your own. To access the explanation and answer for this second exercise, click the provided hyperlink.
calculated height Hc
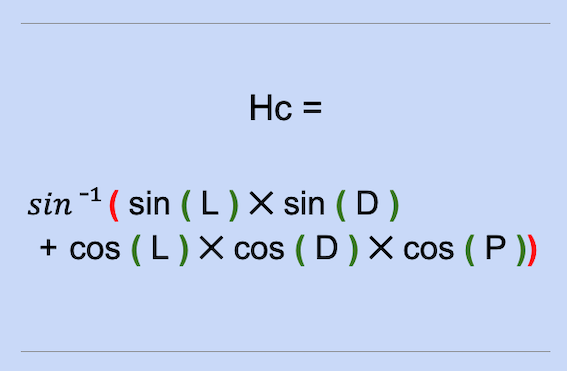
- L = 19° 46′ N
- D = 21 ° 09′,1 S
- P = 39 ° 06‘, 2 (NE)
𝑠𝑖𝑛 ¯¹ ( 𝑠𝑖𝑛(𝐿)
✕ sin(𝐷)
➕ cos(𝐿)
✕ 𝑐𝑜𝑠(𝐷)
✕ 𝑐𝑜𝑠(𝑃))
Indeed, after finding Hc, we are going to calculate Zv.

sun’s altitude and azimut calculation:
Zv

L = 19° 46′ N
D = 21 ° 09′,1 S
Hc = _ _ ° _ _ ‘, _ (Hc we found above)
cos ¯¹ ( ( sin (D)
ー sin (L)
✕ sin (Hc) )
➗( cos (L)
✕ cos (Hc) ) )
Z = _ _ _ , _°
P = NE or SE ⟹Sun in the East ⟹ Zv = Z
P = NW or SW ⟹Sun in the West ⟹ Zv = 360°- Z