Logarithms tables and celestial navigation: the purpose is to calculate the height of the sun (Hc) without a scientific calculator.
This calculated Hc is pivotal in achieving the primary objective of this website, which is to determine your line of position (LOP).
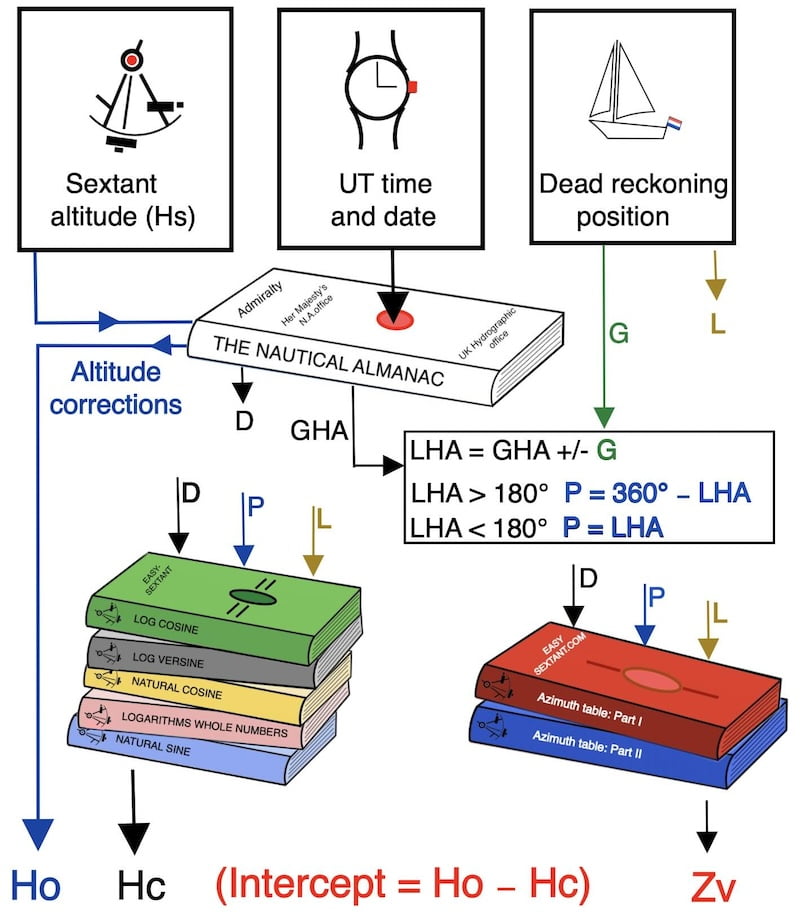
Firstly, these five tables, developed by the author, should be used in chronological order to gradually fill in the spreadsheet and obtain the calculated height of the sun.

Explanation of the logarithm tables.
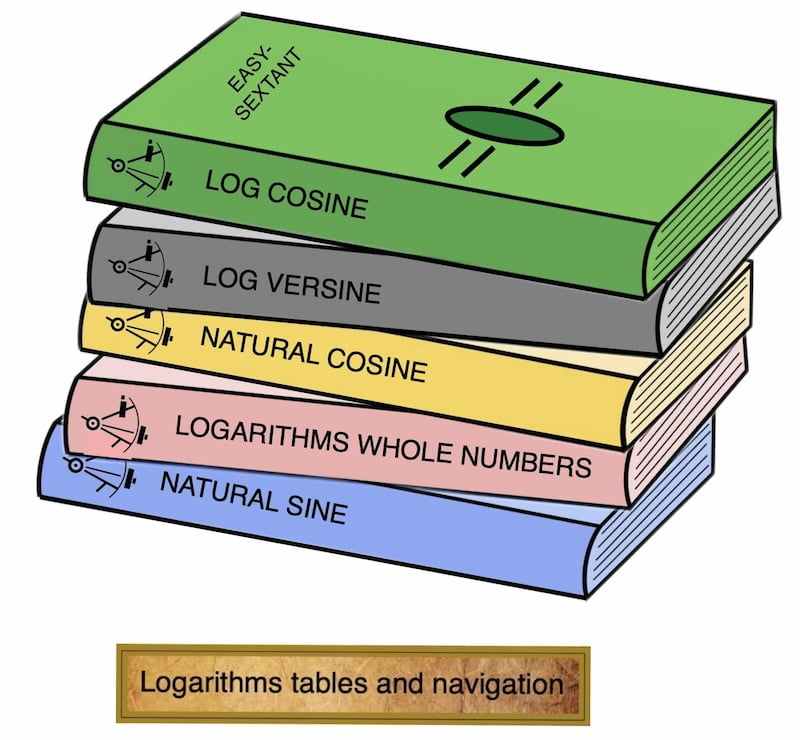
Overall, the use of logarithm tables will replace multiplication with addition.
Additionally, we will find an example and two exercises completed below. (the necessary pages of the tables included).
The idea is to continue with the concept of the D.R. position, and intercept but we no longer use the rule of signs (positive or negative)
Consequently, it will be replaced by the notion same name or not same name. (for examples on this page)


Method
The logarithm tables
Also, we adhere to the same Saint-Marc-Hilaire method.
Furthermore, do not confuse it with the American HO 249 tables for aviation, which are based on different methods and are less precise.
Hence, these logarithm tables do not depend on time either.
The five tables
The logarithm tables and natural sine and cosine tables
The five tables necessary to obtain the calculated height (Hc)
- Table 1: log cosine
- Table 2: log versine
- Table 3: natural cosine
- Table 4: logarithms of whole numbers
- Table 5: natural sine

The author developed these tables with the help of Google Sheets.
The tables are relatively easy to use and should be arranged in order before beginning calculations on our worksheet.
Example of the five tables here:

Logarithms tables and celestial navigation:
Tables of logarithms aim to replace multiplications with additions in order to manipulate large numbers. By performing an addition by hand instead of a multiplication, one can replace the use of a calculator.
To convert natural numbers to logarithmic values, you need to use Tables 1, 2, and 3, then add these values together. Finally, Table 4 can be used to convert the logarithmic result back to a natural number.
Table 4 (logarithms of whole numbers)
The table 4 is not intuitive, but it is easy to use once one knows the rules for using it.
In fact using tables as a tool, one does not need more knowledge in the sometimes very complicated world of logarithms.
Interpolation
It may happen that the input data into the table does not exactly match the values present in the table. In this case, it is necessary to use linear interpolation techniques between two values of the table.
You can estimate these interpolations and tolerate small errors
Use of tables
You can use these tables for the sun, moon, planets, and stars.(maximum Latitude and Declination 68° North and South) and and these tables are not time-dependent.

Logarithms tables and celestial navigation: short summary
Indeed, in this course, you will find a total of four exercises with the logarithm tables, and the necessary pages of the tables and solution included.
Also, the interactive worksheet for the tables provides access to the these four exercises on the following pages:
1) example Hc with the logarithm tables
2) Two exercises Hc with logarithm tables and solutions
Once you have gone through them and become familiar with them, you can test your skills on the seven remaining exercises in the exercise section..
You need to purchase the PDF answer files of the remaining exercises in the store and they come with the full download version of the tables.
I printed these tables along with the azimuth tables, using only one XL cartridge, or you can check with your local printing house.
This is an exceptional tool, but you need to be very organized!

For the purists, I explain how I established the worksheet using the Douwes formula, but you can directly go to the example of how to use the logarithm tables.
Douwes introduced the function Versine: (Versine is is always positive) Explanation of the Douwes formula. Dutch mathematicians and astronomer (1712 – 1773)