On this page Sun’s altitude and logarithm tables at sea, we will find a fully worked-out example of how to calculate the height of the sun (Hc) using logarithm tables at sea.

In fact, observers who see the sun at the same altitude are on the same position circle. (Red Circle)

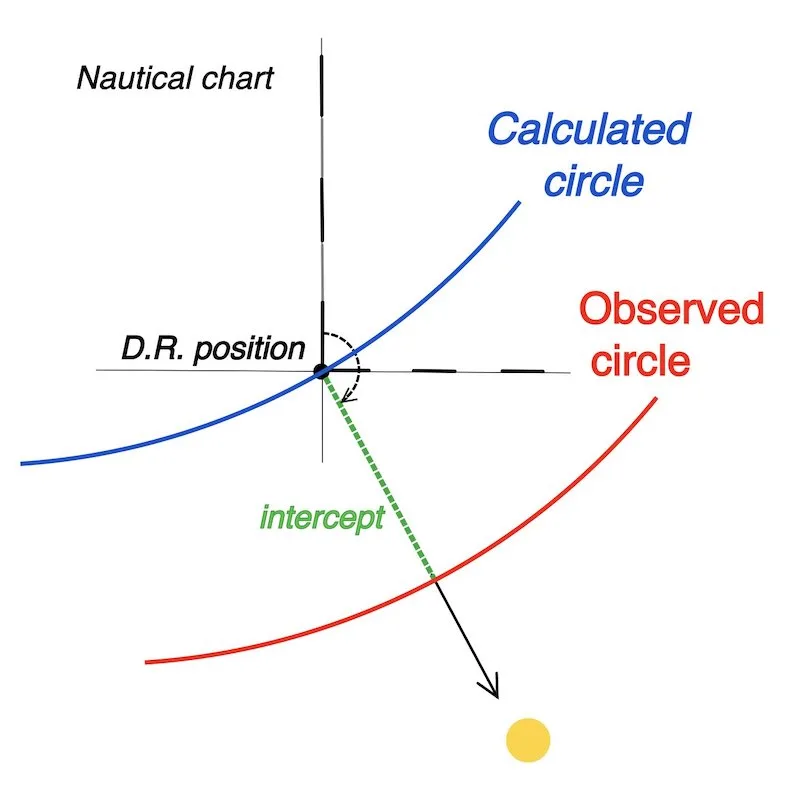
We can also calculate the sun’s altitude from our DR position, resulting in a position circle for the same calculated altitudes (Blue Circle)
On this page, we focus on how to calculate the height of the sun with our D.R. position (Blue circle) using logarithm tables.

Note: Under normal navigation circumstances, the circles are so large that locally we can regard them as straight lines
For further information, please refer to the principles of the sun sight.


Sun’s altitude and logarithm tables at sea: using the tables
Example and solution
In fact, the inputs obtained in the first part of the worksheet necessary to find the calculated height (Hc) are:
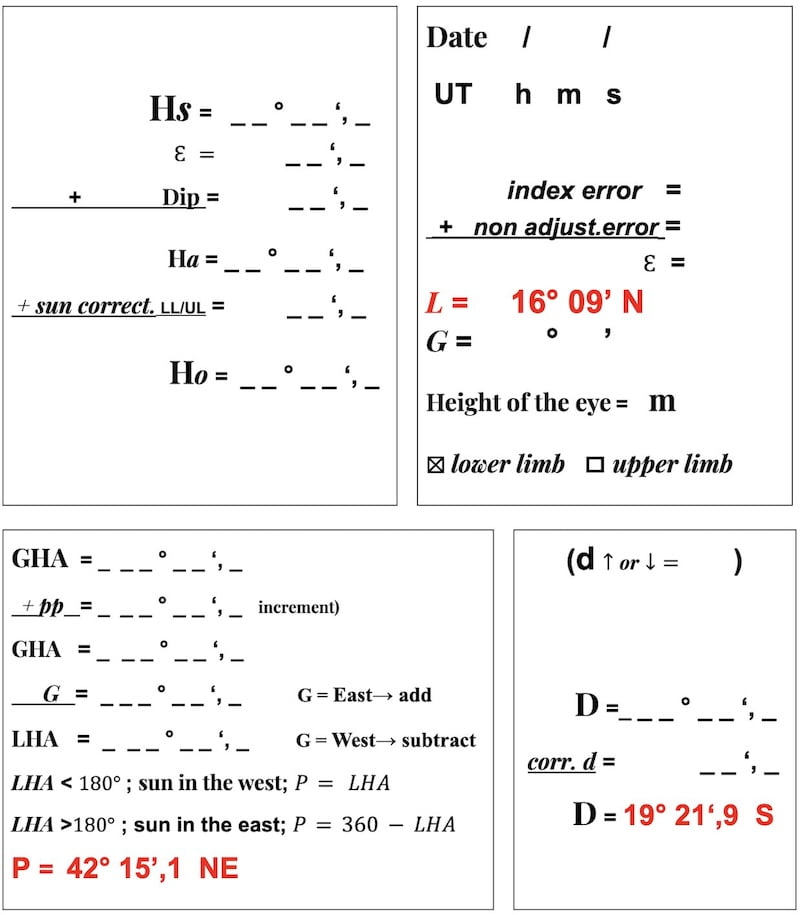
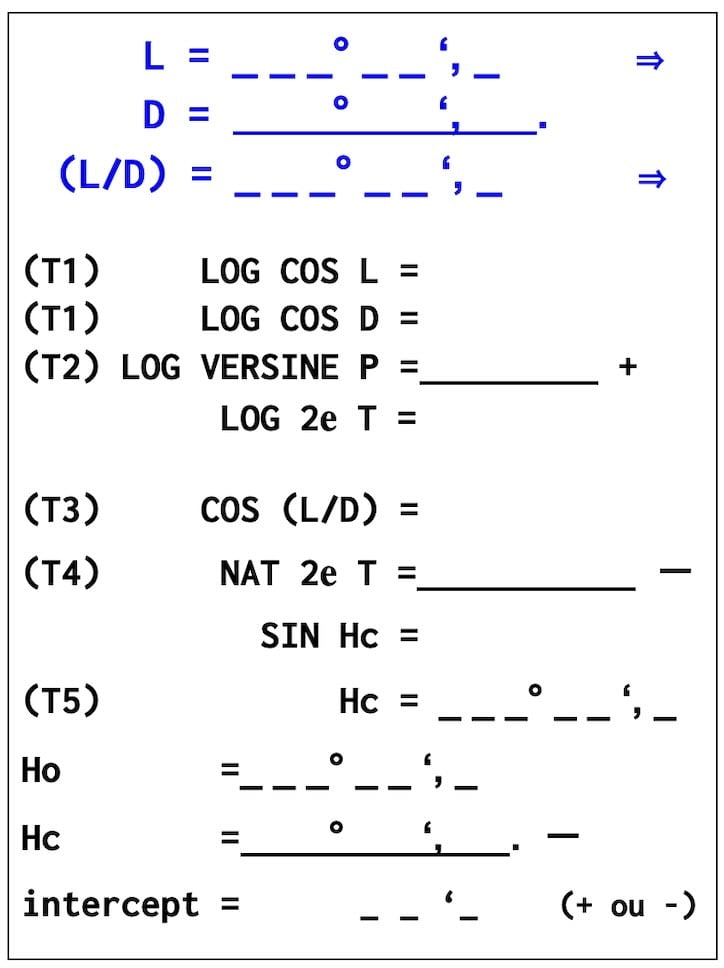
L = 16° 09′ N (D.R. latitude)
D = 19°21′,9 S (declination of the sun)
P = 42°15′,1 (NE) (polar angle)
Sun’s altitude and logarithm tables at sea:
Indeed, you can always view the original PDF files pages for this exercise that are available for download.(see below)
Sun’s altitude and logarithm tables at sea:
Table 1
log cos L
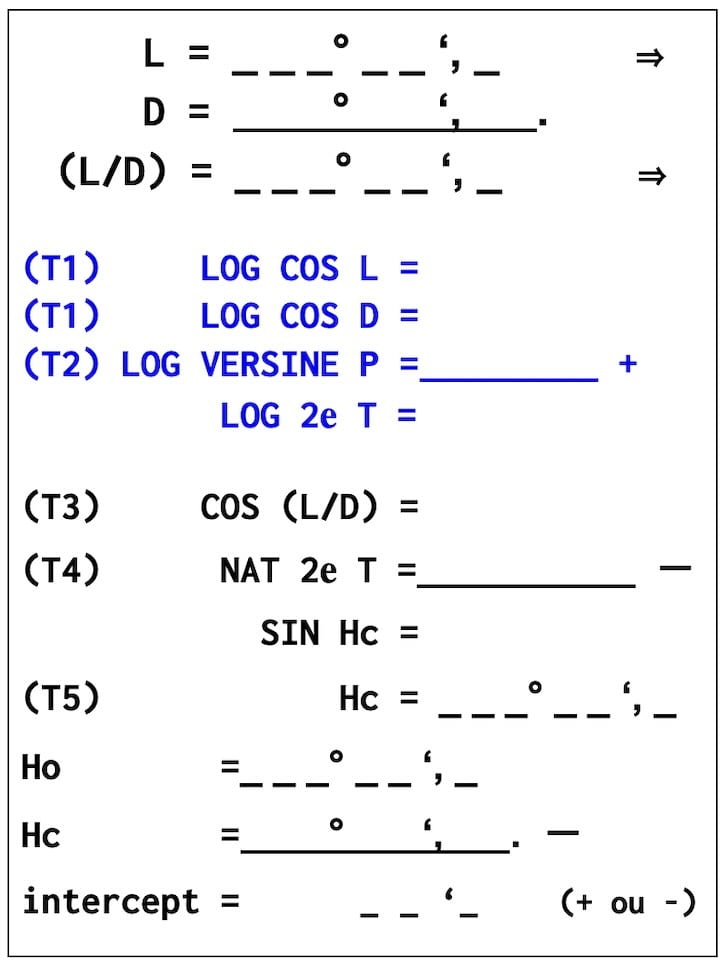
Latitude = 16°09’N

log cosine 16° 09′ on our scientific calculator gives us -0.017485.
It is nevertheless much more convenient to put these sorts of logarithms in the form of positive quantities.
American tables are then presented in the following form:
10 + (-0,017485) = 9,98251
Log cos L = 9,98251
Log cos D
Declination = 19° 21′,9 S
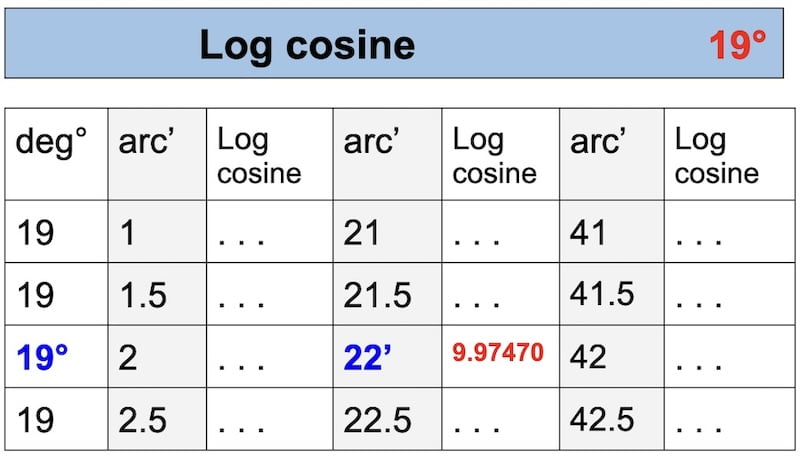
Log cos D = 9,97470
Sun’s altitude and logarithm tables at sea:
Table 2
Log versine P
Polar angle = 42° 15′,1
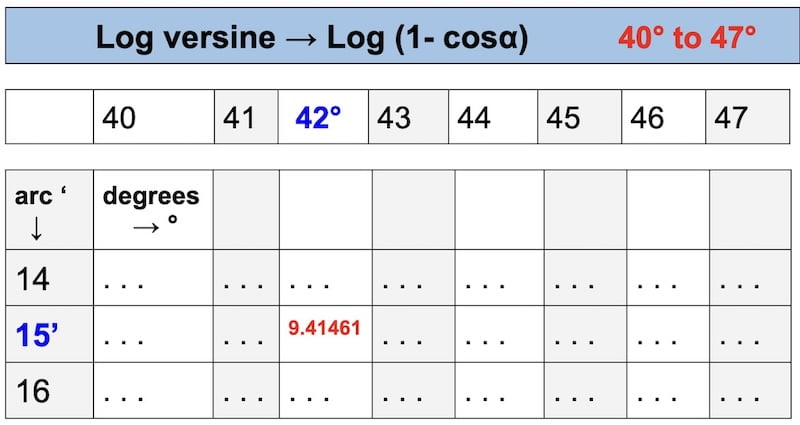
Log versine P = 9,41461

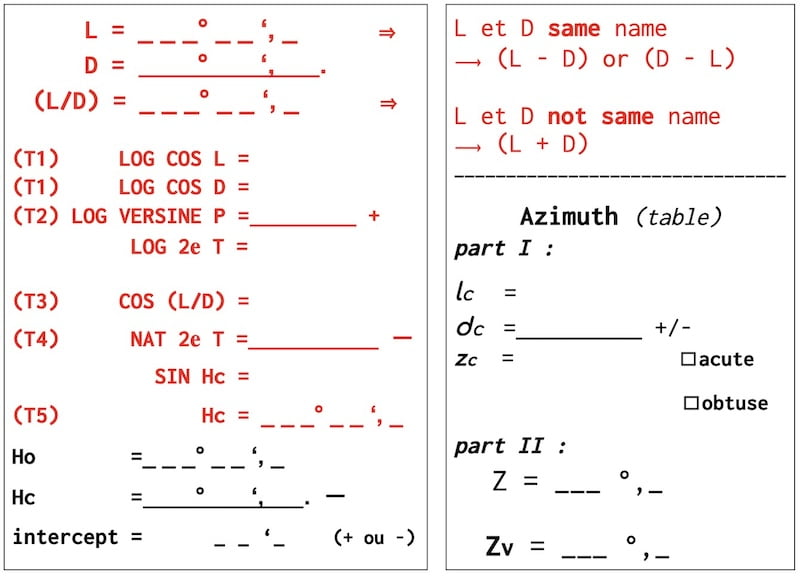
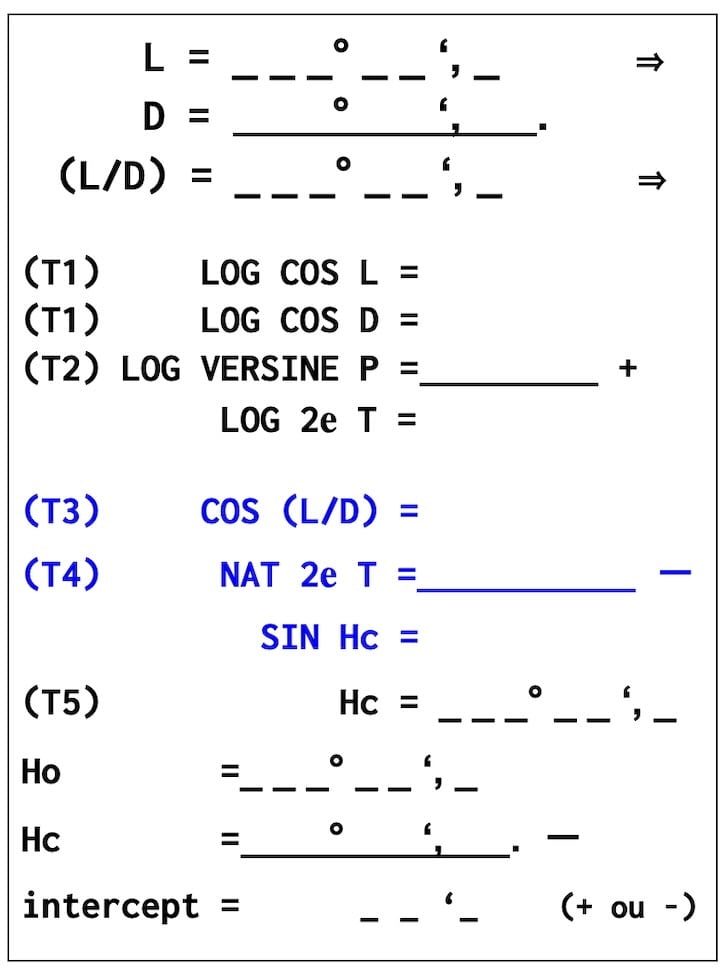
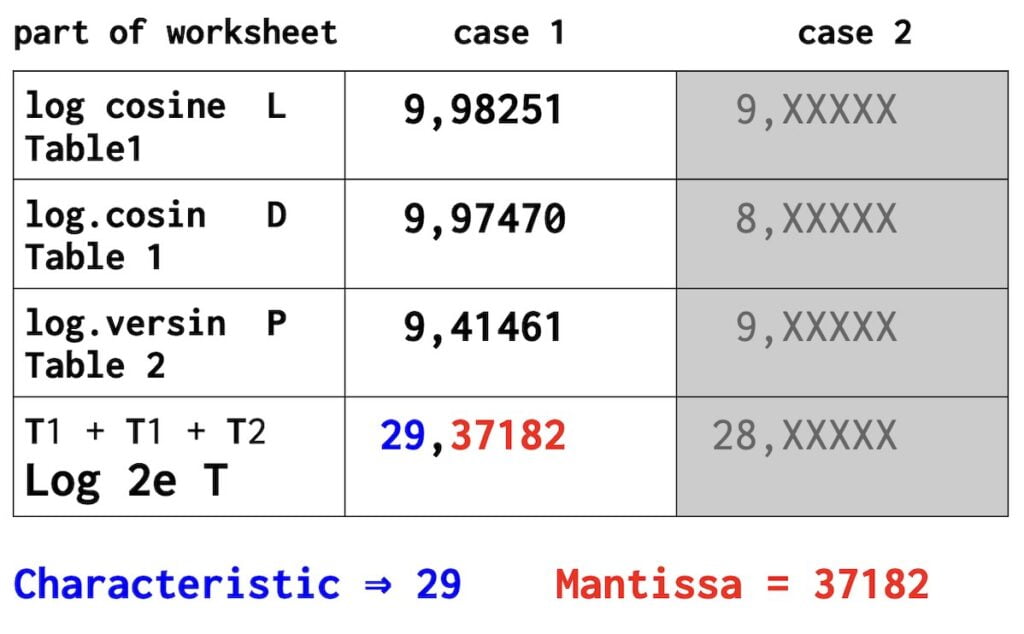
1T 1………….LOG COS L = 9,98251
2T 1………….LOG COS D = 9,97470
3T 2….LOG VERSINE P = 9,41461
_______________________________+
………………LOG 2e Term = 29,37182
Sun’s altitude and logarithm tables at sea: Table 3
Table 3

See: same name/not same name with 4 examples

L et D same name
⟶ (L – D) or (D – L)
The answer must always be positive
L et D not same name
⟶ (L + D)
The answer must always be positive
L = 16°09’N
D = 19°21′,9 S
L and D not same name: ( L+D ) = 16° 09′ + 19°21′,9 = 35° 30′,9
cos (L + D)
( L + D ) = 35° 30′,9
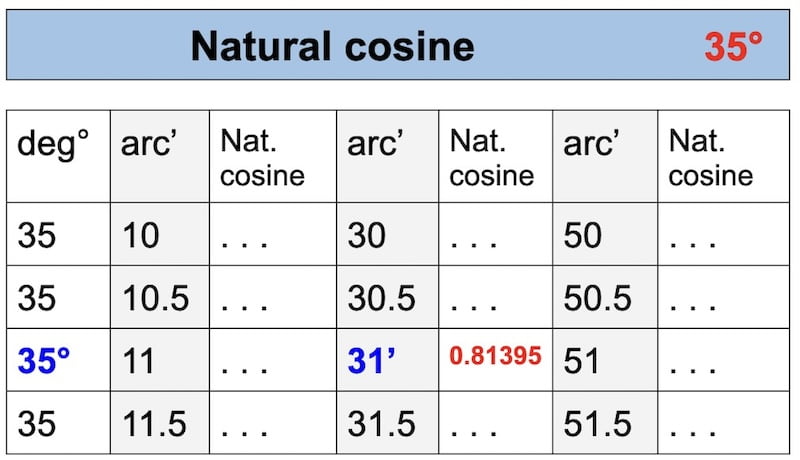
T 3. COS (L + D) = 0,81395
Sun’s altitude and logarithm tables at sea:
Table 4
Log 2e Term to Nat 2e Term
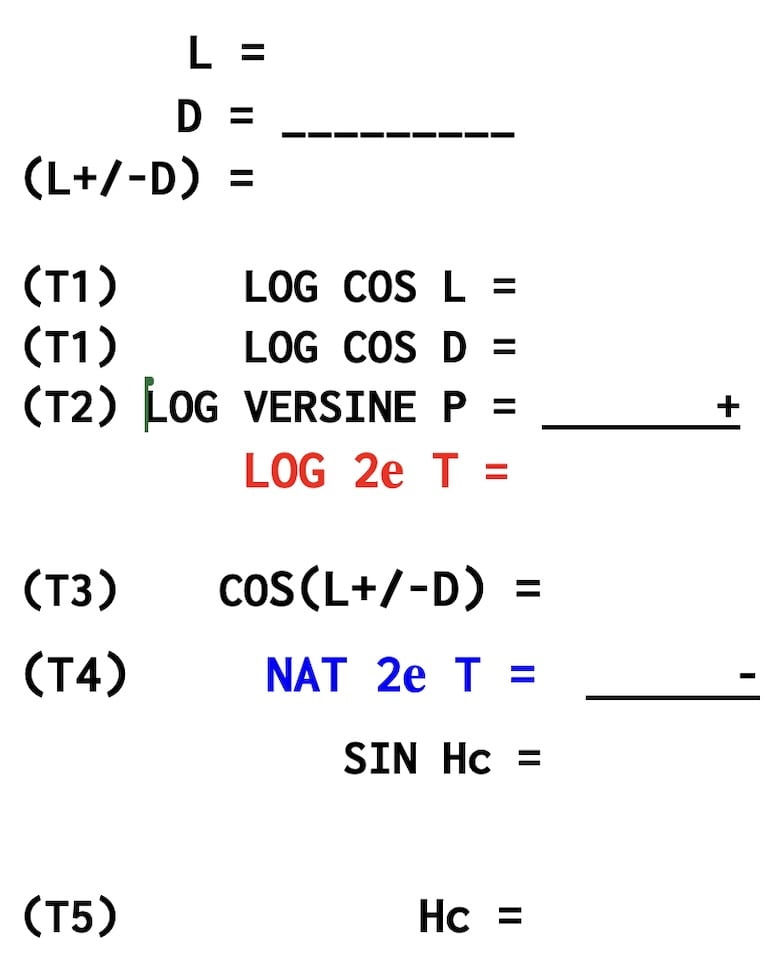
Firstly, with the Mantissa we will search for the whole number in table 4 (logarithms of whole numbers.)
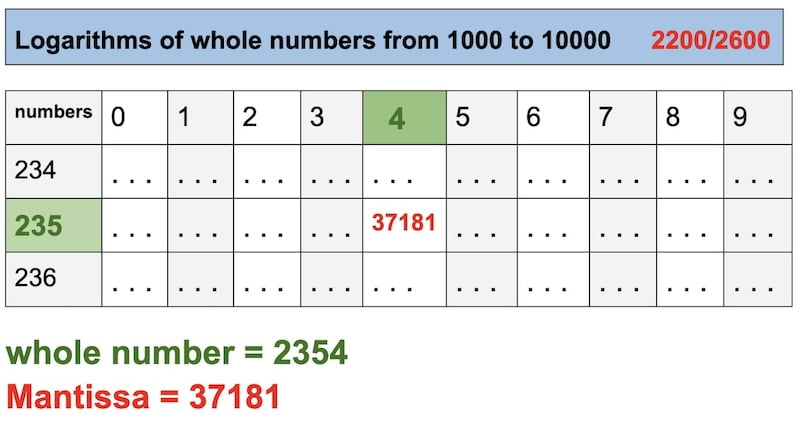
Finally, after finding the whole number (2354), we have to put the comma!

natural 2e term = 0,2354
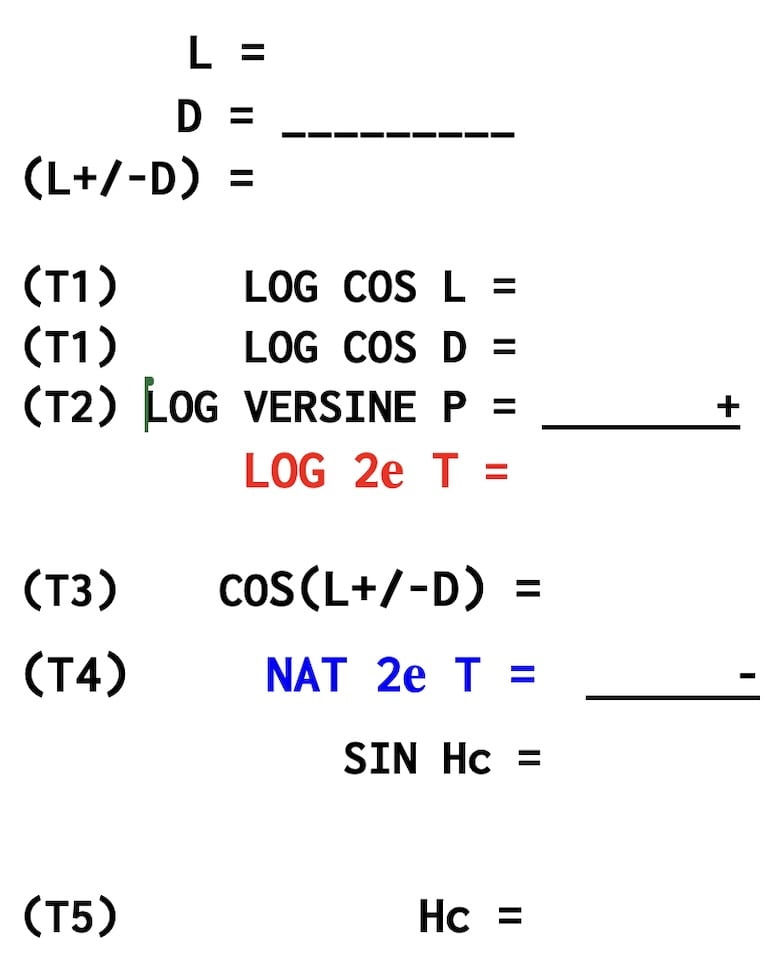
T 3………..COS (L +/- D) = 0,81395
T4………………..NAT 2eT = 0,2354
_________________________ ⎼
…………………….. SIN Hc = 0,57855
Table 5
Sin Hc = 0,57855
Finally, you have to look up this value ( 0,57855 ) in Table 5 to find the calculated height. Sometimes it needs some interpolation.
SIN Hc = 0,57855
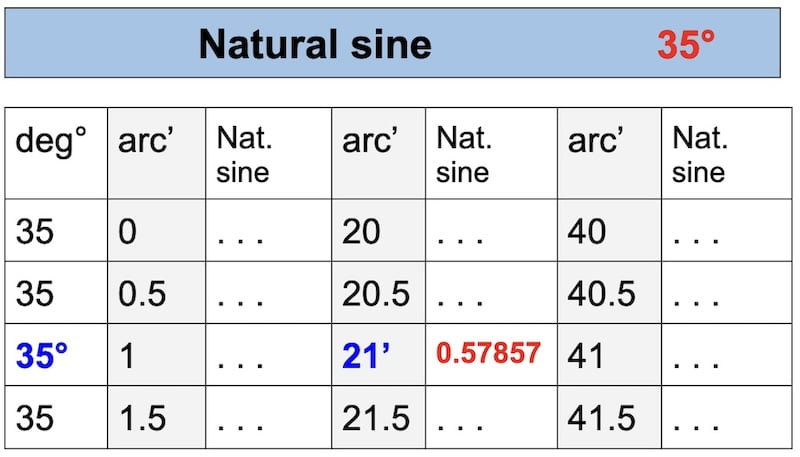
T 5………. Hc = 35° 21′
In fact, with calculator: arcsin (0.57855) = 35° 21′

Sun’s altitude and logarithm tables at sea:

Brief summary
Firstly, in celestial navigation, navigators measure the angle between the horizon and the sun using a sextant to determine the observed height or the observed altitude.
Additionally, celestial navigators obtain the calculated height, which is determined using trigonometric formulas considering the observer’s geographic coordinates, the sun’s declination, and other relevant parameters.
comparing the observed height with the calculated height.
Furthermore, navigators can correct any potential errors and find their Line of Position by comparing the observed height with the calculated height.
Moreover, this comparison between the observed height obtained from a sextant and the calculated height plays a crucial role in celestial navigation, allowing navigators to refine their calculations and improve the accuracy of their dead reckoning position.
By comparing the observed height with the calculated height, navigators can provide a reliable method for determining a ship’s location when other navigational aids are unavailable.