Observed sextant height of the sun: On this self-instruction platform, you’ll discover the significance of sextant corrections through a series of eight identical exercises, commencing with the LA ROCHELLE exercise.
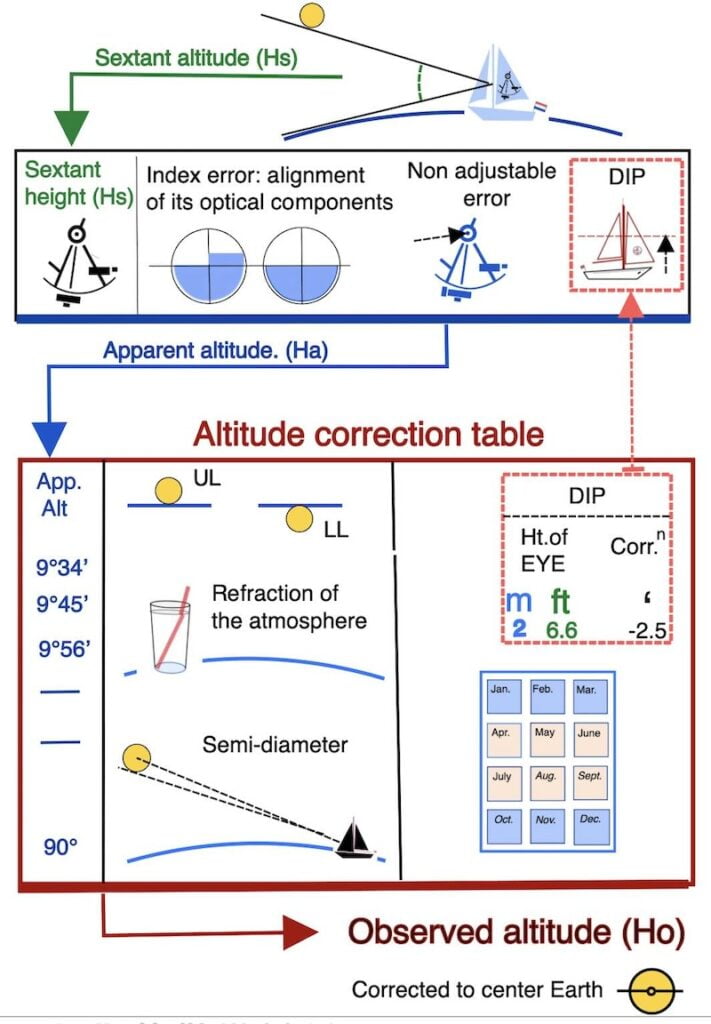
On this page, we explore the theory behind determining the observed height of the sun. If you’ve been following the course, you’ve already learned about apparent height and its calculation.
Observed sextant height of the sun: Apparent height (Ha) to observed height (Ho)

Altitude = Height
This step involves correcting for atmospheric refraction as well as compensation for the varying diameters and distances of both the Sun and the Earth throughout the year.
Consequently, these adjustments collectively result in the final observed height, measured from the center of the Earth to the center of the Sun.

Observed sextant height of the sun:
RED section of the worksheet explained on this page
Introducing various astronomical phenomena that can affect the accuracy of observing the Sun.
After correcting errors specific to the sextant and the height of the eye above the horizon to obtain the apparent height, it is necessary to account for various phenomena, such as refraction, semi-diameter, and parallax.
This process ensures the accurate measurement of the center of the Earth to the center of the sun, and is referred to as the observed height.
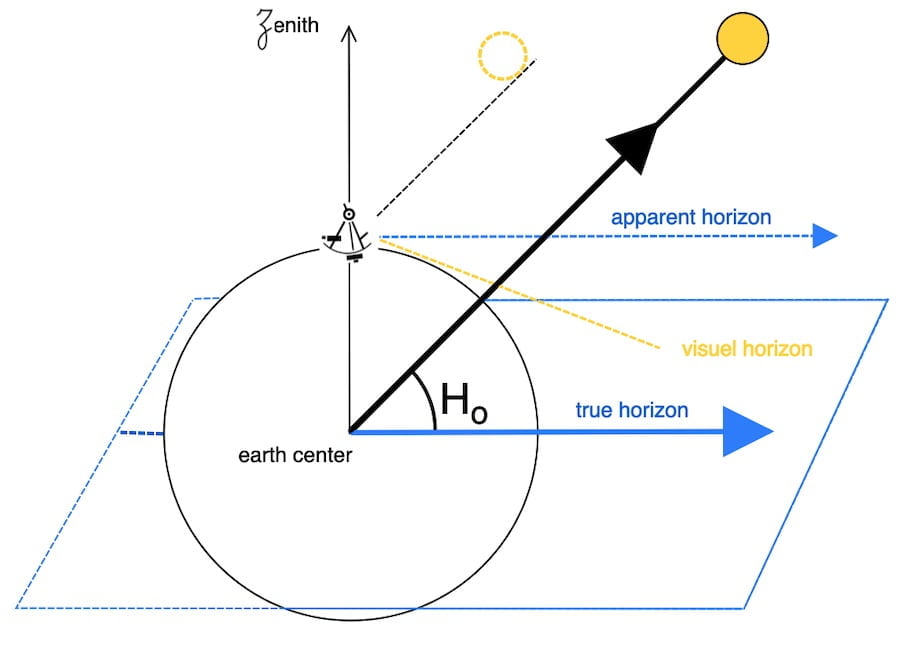
apparent height (Ha) to observed height (Ho):
In fact, the altitude correction table compiles the three errors mentioned above!
They are interesting, but you don’t need to remember them!!
Furthermore, there is a small overview of these 3 phenomenas at the bottom of this page

Observed sextant height of the sun:
Refraction, Parallax and semi-Diameter
While these errors are fascinating, there’s no requirement to memorize them!
Once more, the altitude correction table summarizes the three errors discussed earlier.
To illustrate, small overview of these 3 phenomena:
Refraction of the atmosphere
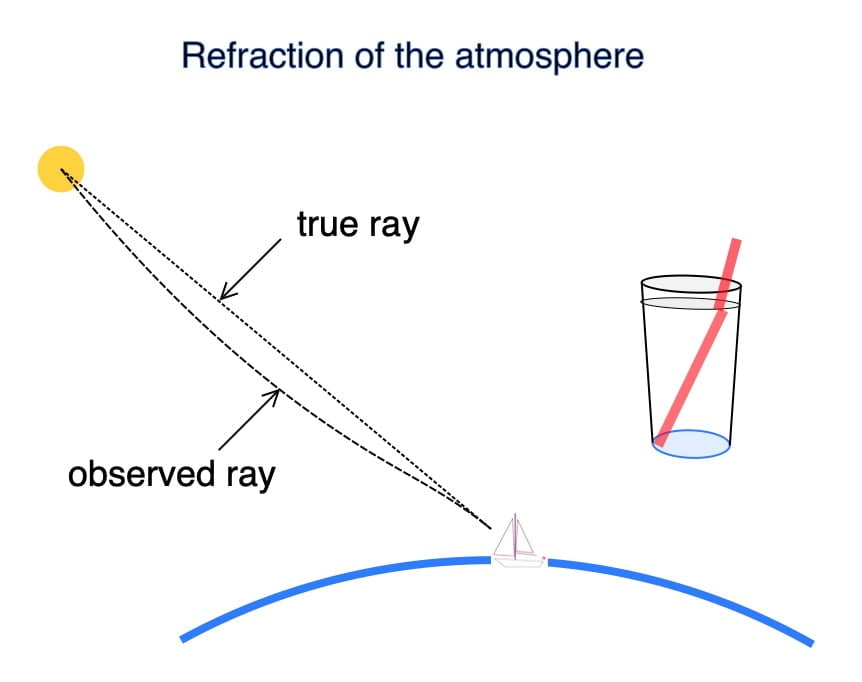
In fact the refraction formula is:
⎼ ( 55,7 ✕ Tan (90° ⎼ altitude sight)) / 60 (always negative)
The effect is that the sun appears to be higher above the horizon than it actually is.
Parallax
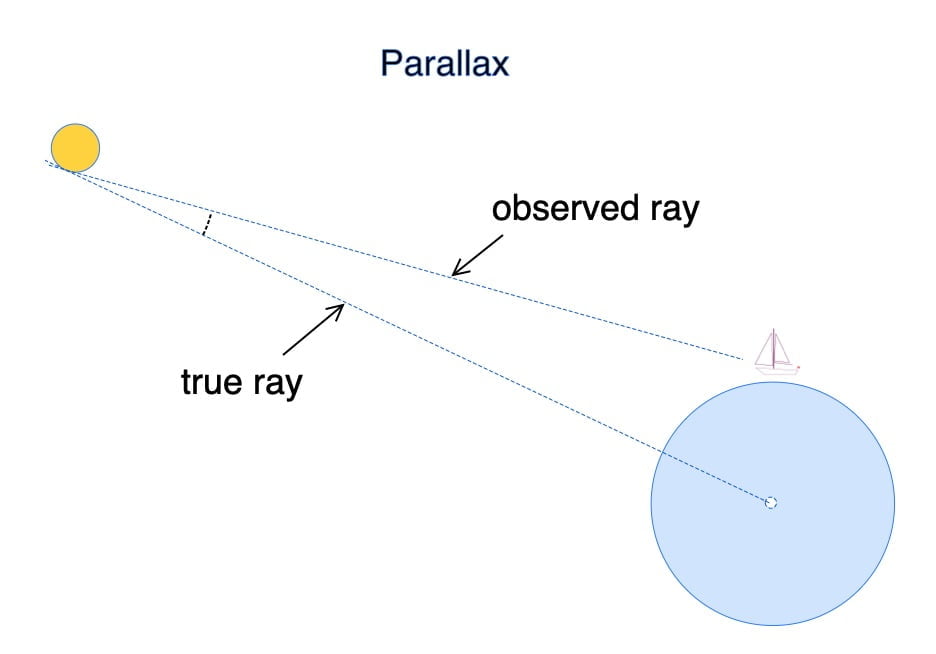
However the parallax is negligible for the sun but important for the moon
Semi-diameter of the sun

To clarify LL/UL (lower limb and upper limb):
To clarify in practice we mesure mostly the lower limb of the sun and not the center

apparent height (Ha) to observed height (Ho):
the distance between the earth and sun changes over the year, so the semi diameter correction angle will change also a little
The term “semi-diameter” is commonly used in astronomy and geodesy to refer to half of the apparent or angular diameter of an object in the sky, such as a planet or star. This is because the apparent size of these objects is usually measured in angular units, such as degrees, minutes, and seconds of arc.
The semi-diameter of the sun 696350 km
Distance at the beginning of January sun-earth = 147,100,000 km
Semi-Diameter Angle = arc Tan ( 696350/147100000) = 16’,3
Distance at the beginning of July sun-earth = 152,100,000 km
Semi-Diameter Angle = arcTAN ( 696350/152100000) = 15’,7
To summarize in the permanent Altitude correction tables from Nautical Almanac, this change in the semi-diameter results in two different correction periods:
The period from October to March, and the period from April to September.

In conclusion, using the altitude correction table is relatively easy.
It compiles the three errors mentioned above.

Observed sextant height of the sun:
The use of the altitude correction tables
10°-90° SUN, STARS, PLANETS
Permanent table of the Nautical Almanac
An example how to use the altitude corrections tables:
- As an example, suppose that the apparent altitude (Ha) of the sun is 20°
- We observed the lower limb of the sun.
- The date of the sight is sometime in June.

The star and planet corrections, as well as the lower limb correction, appear on this page in the Nautical Almanac.
You can find a more elaborate altitude correction table below. (For sun only)
So now we look in the altitude correction table and then we find in the period april-sept. with Ha = 20° and using the lower limb of the sun:
Ho = 13′,4
Hence, how it was calculated 😆 :
During the period from April to September, the average semi-diameter is 15,9 minutes.
Taking into account the refraction of ⎼2′,5 minutes
(calculated as ⎼ ( 55.7 ✕ tan(90⎼20)) /60 =
The final result is ( 15′,9 + ⎼2′,5 ) = 13′,4
Undoubtedly it’s worth noting that the parallax of the sun can be disregarded in this context.
Observed sextant height of the sun:
Example: Calculation of Observed Sextant Height of the sun:
