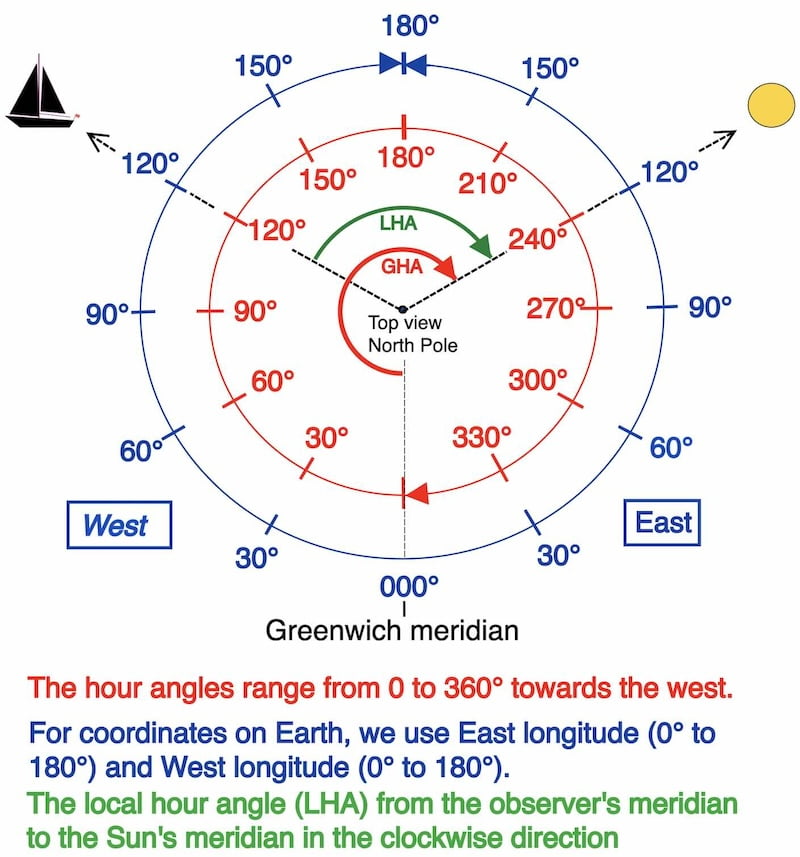
On this page discussing Local Hour Angle and Astro Navigation, we correlate the estimated longitude of the observer with the Sun’s Greenwich Hour Angle (GHA), as obtained from the Nautical Almanac, which is referred to as Local Hour Angle (LHA).
For mathematical reasons, we transform the local hour angle L.H.A(0° to 360°) into the polar angle P (0° to 180°), which requires a specific condition explained in detail on this page and use it in our mathematical formulas to obtain the calculated height and Azimuth of the sun.
After reading this page, remember that the most important section to begin with on this website is the LaRochelle exercise if you want to learn how to calculate the Line of Position (LOP), which forms the foundation of celestial navigation.

Before reading this page, you should review the theory of the Sun’s
Declination and the GHA (Greenwich hour angle) page.

GHA TO LHA
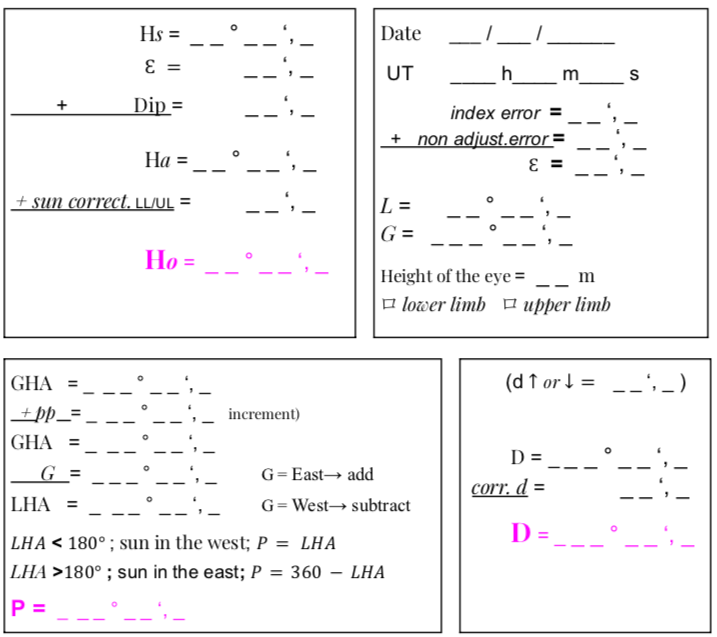
GHA = _ _ ° _ _ ‘, _
+pp = _ _° _ _ ‘, _
GHA = _ _ ° _ _ ‘, _
___________________
G = _ _ ° _ _ ‘, _
_____________________
LHA = _ _ ° _ _ ‘, _
See: how to calculate LHA and P
G is longitude of dead reckoning position
In fact G: add if East / subtract if West
After finding LHA, how to deduce the polar angle (P) ?
ロ LHA < 180°
sun in the West P = LHA
ロ LHA > 180°
sun in the East P = 360 – LHA
P = _ _ ° _ _ ‘, _
NE / NW / SE / SW
(To clarify, for example P = _ _ ° _ _ ‘, _ SE , We are situated in the Southern Hemisphere, and the sun is in the East at the time of our observation.
Here are four practical examples of calculating the Local Hour Angle (LHA) and the Polar Angle (P).

Theory of Local hour angle (LHA) and Polar angle (P):
Local hour angle (LHA)
In addition, we establish the angle between the meridian of the dead reckoning position (G = estimated longitude) and the meridian of the sun
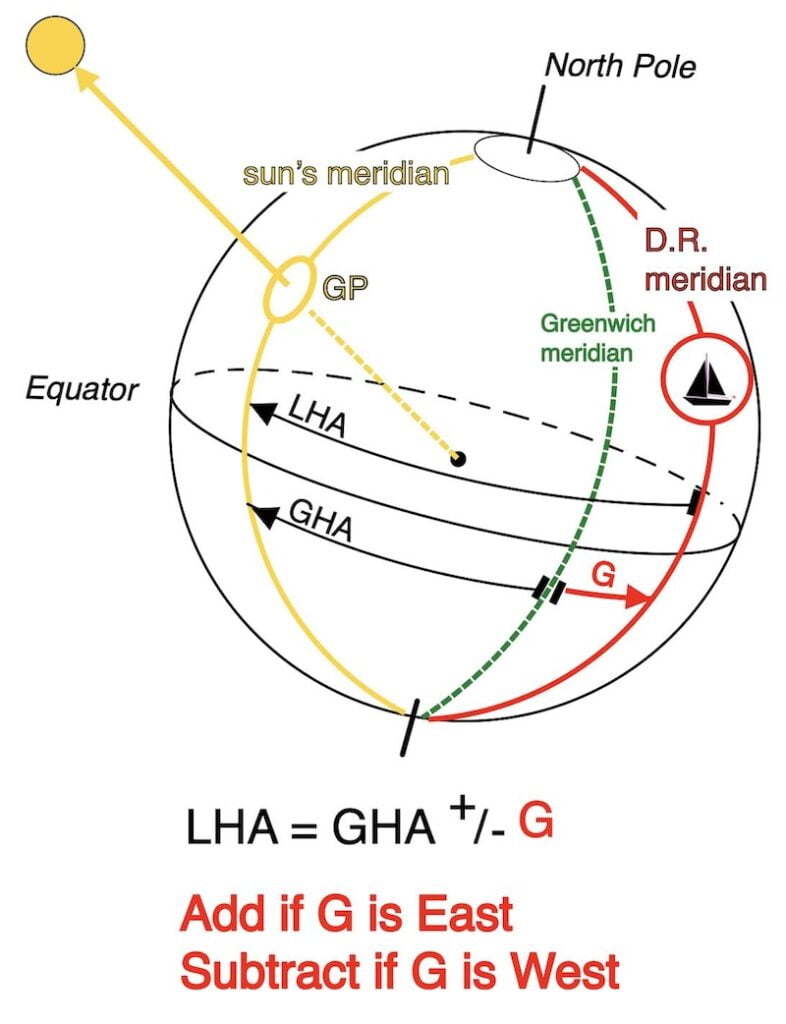
LHA = GHA + G
To clarify, the convention of signs:
North latitude (L) and North Declination (D) +
South latitude (L) and South Declination (D) ⎼
Longitude (G) East +
Longitude (G) West ⎼
Furthermore, by applying the convention signs, we can conclude that we must add East longitude and subtract West longitude for the relation LHA = GHA + G.
GHA = _ _° _ _’, _
___________________
G = _ _ ° _ _ ‘, _
_____________________
LHA = _ _ ° _ _ ‘, _
In conclusion, add G if East and subtract if West
Polar angle (P)
Instead of using the local hour angle LHA (0° to 360°) one can use the polar angle which counts between (0° to 180°) at the following condition:
LHA < 180°
⟹ Sun in the West ⟹ P = LHA
LHA > 180°
⟹ Sun is in the East ⟹ P = 360° ㆒ LHA

Local hour angle and astro navigation:
the spherical triangle
Additionally, the polar angle (P) is one of the 3 keys to the trigonometric resolution of the triangle .
Although the resolution of the spherical triangle with fundamental formulas such as the cosine formula can be achieved, the process becomes even more complex when mixing between equatorial coordinates and horizontal coordinates.
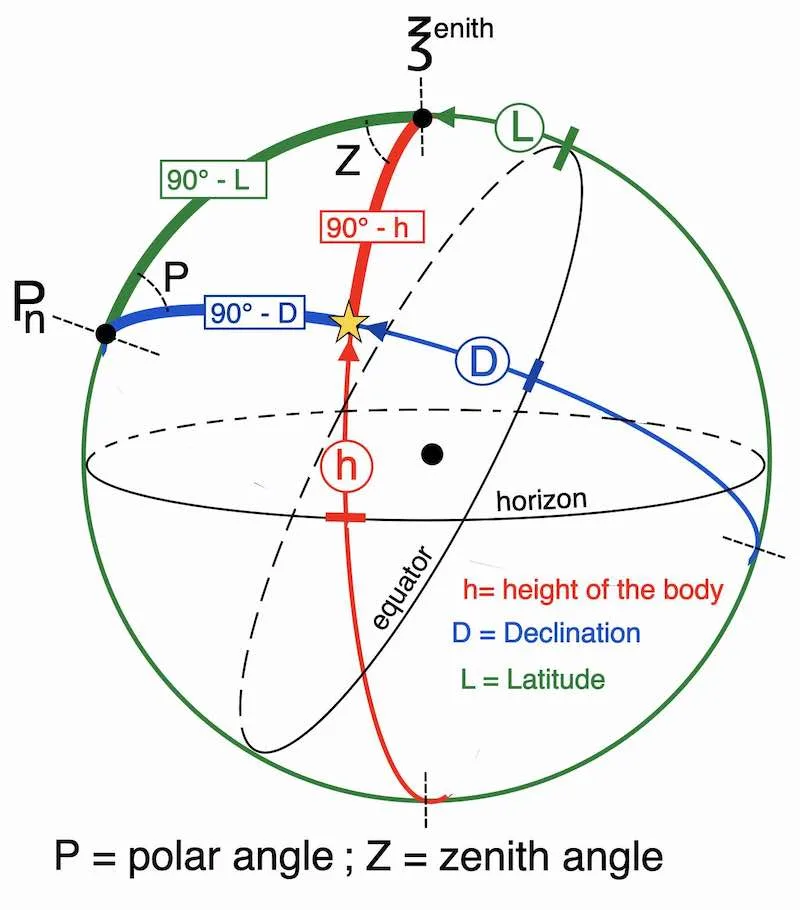
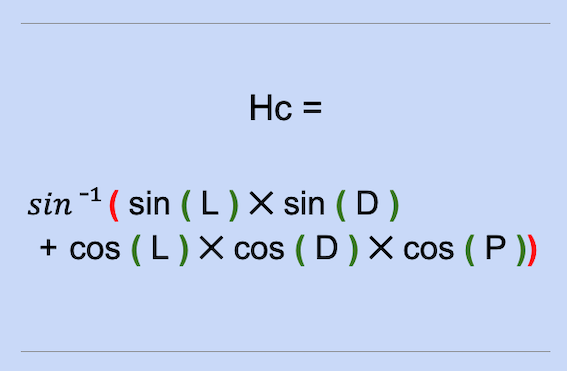

Indeed, solving the spherical triangle requires a good understanding of trigonometry, and this generates the formula with P, D, and L that can be used to calculate the height of the sun.
In summary, when calculating a line of position at sea or in an examination room, the understanding of the trigonometric resolution of the spherical triangle appears to be of relatively minor importance.

conclusion
I don’t insist on the fundamental accomplishments of these particular formulas
Moreover, there’s no need to memorize the formulas for this calculation since they are already included in our worksheet.
Hence what matters is the correct filling of the classic St Marcq Hilaire worksheet including the formulas with respect for the signs.
And this takes practice…