This page explains the ancestral celestial Douwes formula, a logarithm-based method featured in the second part of my worksheet

Begin with the Celestial navigation and Logarithme option page — the starting point of the “Logarithmic” menu, which includes all essential links and will take you back to this page when appropriate.
In fact, this formula allows you to calculate the sun’s altitude using only logarithm tables, without the need for a scientific calculator.
The main objective of this website is to assist in determining your sea position with a sextant, with a primary focus on utilizing a scientific calculator, although the option to employ logarithm tables is also available.
However, understanding Douwes’ formula is not required to use the tables.

Hence, you may skip this page without any difficulty in using the tables.

The Hidden Beauty of the Cosine and Logarithms
Logarithms are very useful because they transform, for example, multiplications into additions, greatly simplifying complex calculations. Before the advent of calculators, this method enabled rapid and precise computations, particularly in astronavigation and trigonometry.
The formula:
The Douwes formula expresses the computed altitude of the Sun as follows:
sin Hc = cos (L±D) − cos(L) × cos(D) × versine(P)
Although Douwes’ formula gives sinHc, it is expressed entirely with cosines and the versine, which makes it particularly suitable for computation using logarithmic tables.
The cosine also offers a major advantage: it always yields a positive value, regardless of latitude. Thus, a southern (negative) latitude poses no problem, whereas the logarithm of a negative sine has no real value. Thanks to this property, formulas based on cosines, such as Douwes’ formula, are better suited for practical calculation.
We start by converting natural values into logarithmic values using the logarithm tables. In this way, multiplications become simple additions of logarithms.
Finally, the results are converted back into natural values using the table of logarithms of whole numbers, which in this context serves as an antilogarithm table.
The Logic of Logarithmic Calculation
Logarithms allow, for example, a long multiplication to be transformed into several small additions.
Let’s take an example: instead of calculating 20 × 300 directly, we proceed as follows:
- Transform 20 and 300 into their logarithmic values using the table of logarithms of integers;
- Add these two logarithms together;
- Then, using the same table (this time as an antilogarithm table), find the real value again.
The result is indeed the same (6000), without performing the multiplication directly.
However, understanding this explanation — though theoretical — is not a necessary step for using the tables effectively.
Explanation of Douwes’ formula

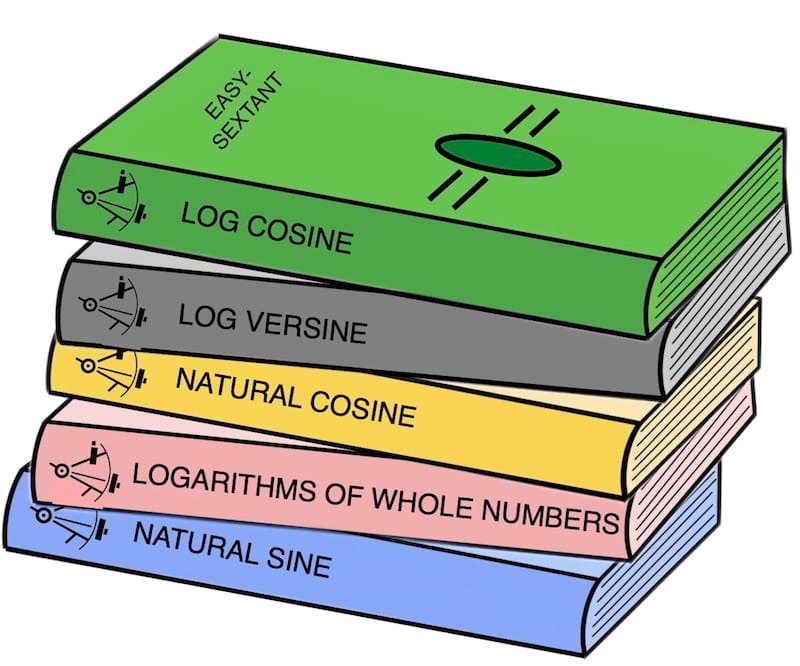
Also, to work with this formula without a calculator we will use the logarithm tables and the natural sine and cosine tables
The formula
L = Dead reckoning latitude
D = Declination of the sun
P = polar angle
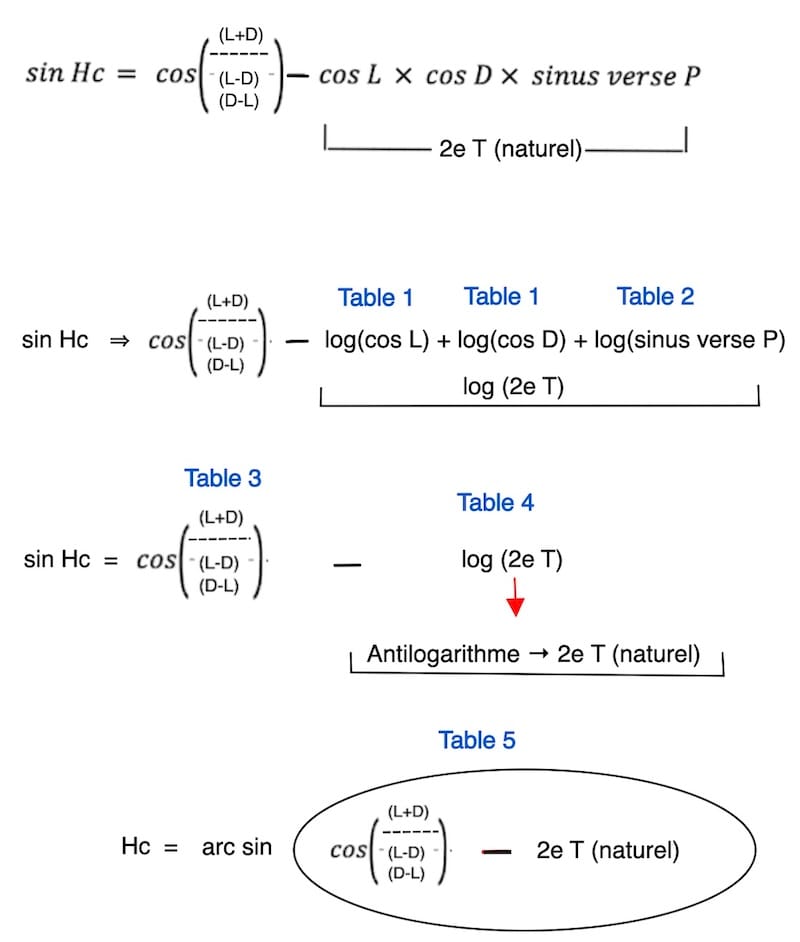
Explanation of the versine
The versine is defined as: versine P = 1 − cos P.
log(versine P) = log(1− cos P)
Table 2 provides the values of the versine directly.
Explanation of (L±D)

See page: SAME NAME/NOT SAME NAME, which is part of the logarithm method. In this section, we do not use the Rule of Signs.

Ancestral celestial Douwes formula:
Explanation of Table 4
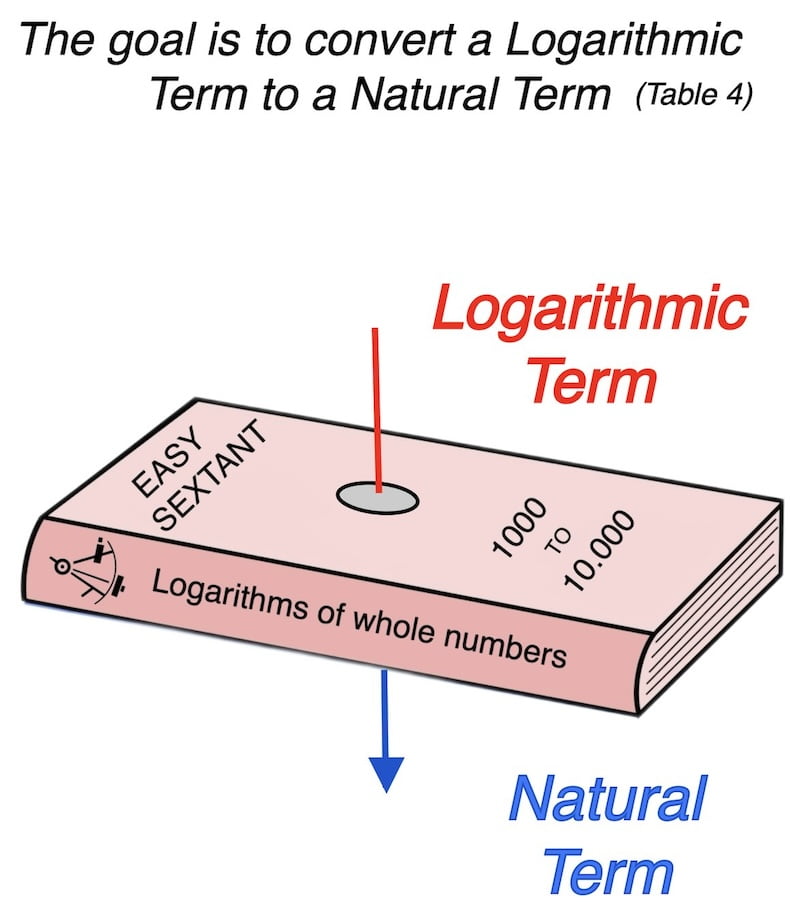
Finally, after finding log of the second term, we will use Table 4 (logarithms of whole numbers) to find the natural second term (antilogarithm).
Explanation of Table 5
Consequently, from the result cos (L±D) − 2nd natural Term = sin Hc, we obtain sin Hc.
example: sin Hc = 0.5
Hc = arcsin (0.5) = 30° (Table 5)

Additionally, here you can find a total of 4 exercises, all fully worked out and provided with the necessary table pages.
example Hc with the logarithm tables
Two exercises Hc with logarithm tables and solutions
La Rochelle Exercise — Logarithm Option
In conclusion
To use the logarithm table of whole numbers, one first looks up the logarithm of a given number, performs the necessary calculations using those logarithmic values, and then uses the same table — this time in reverse — to find the corresponding number (the antilogarithm).
However, in the method presented here, other tables are used to determine logarithmic values such as log(cos L) or log(versine P), and finally, the table of logarithms of whole numbers is used as an antilogarithm table to recover the natural value.
Logarithm tables were once an essential tool in fields such as mathematics, engineering, physics, and navigation, where precise and efficient calculations were required.
However, with the advent of electronic calculators and computers, the use of logarithm tables has declined significantly. Modern computing devices can perform logarithmic calculations quickly and accurately, making manual searches in tables largely unnecessary.
Yet, a trained navigator can be just as fast as someone using a calculator.
On the webpage Links and Helpful Resources, you can find a short history of the sextant.
