
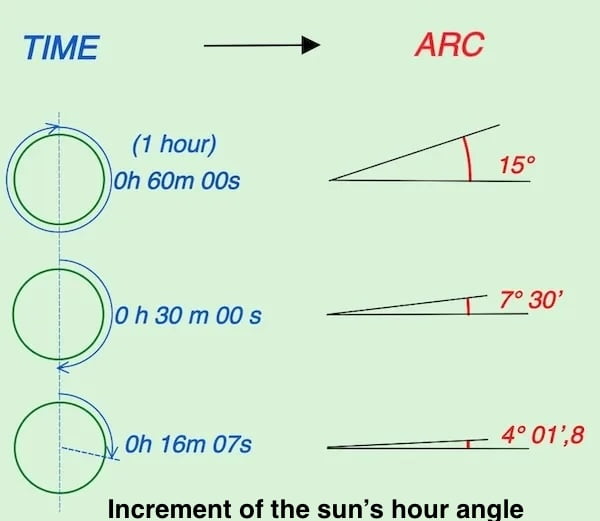
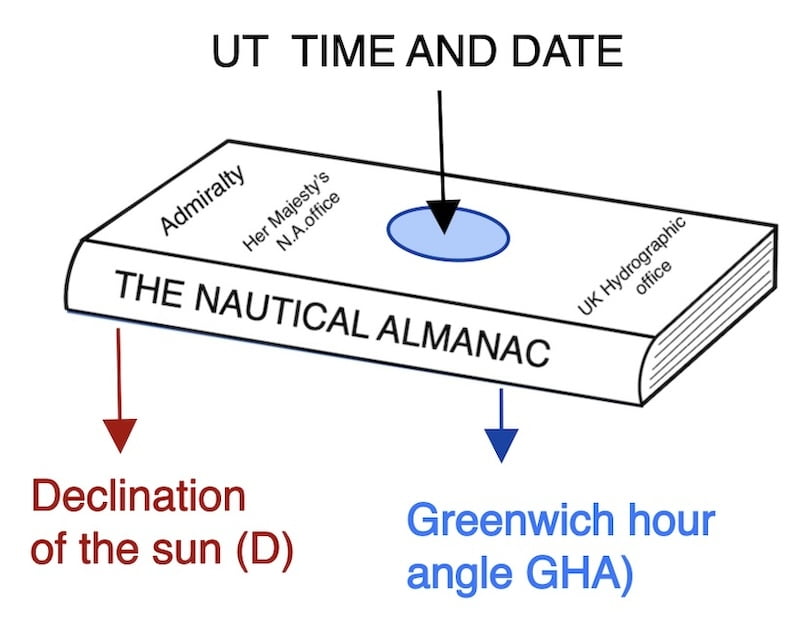
This page on the increment of the sun’s hour angle is designed to.calculate the GHA (Greenwich Hour Angle) for the exact moment of a sextant observation by initially acquiring the GHA from the beginning of the whole hour as specified in the nautical almanac.

After reading this page remember the most important page to start with is the LaRochelle exercise.
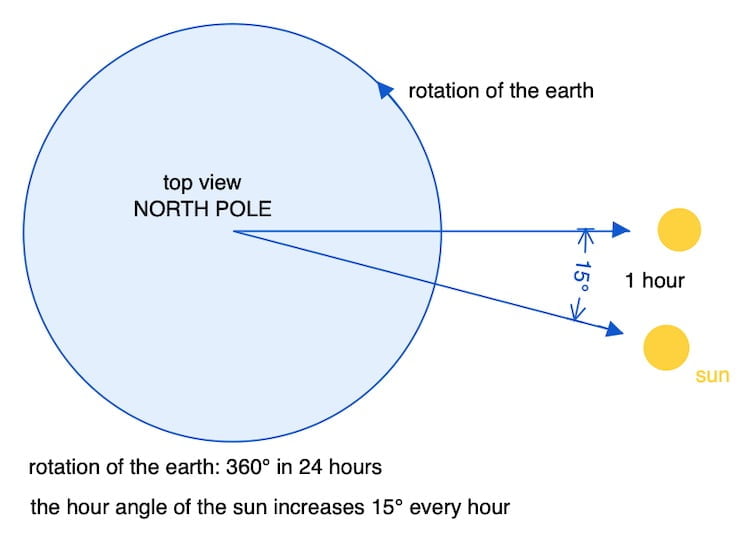
The hour angle of the sun increases 15° every hour
(0,25° per minute)

Increment of the sun’s hour angle
The increment of the sun’s hour angle exhibits a linear increase at a rate of 0.25 degrees per minute, known as the ‘time to arc.’ This expression captures the relationship between time and the corresponding solar angle. In our context, precise calculations necessitate determining the increase of this angle (arc) with accuracy down to the second
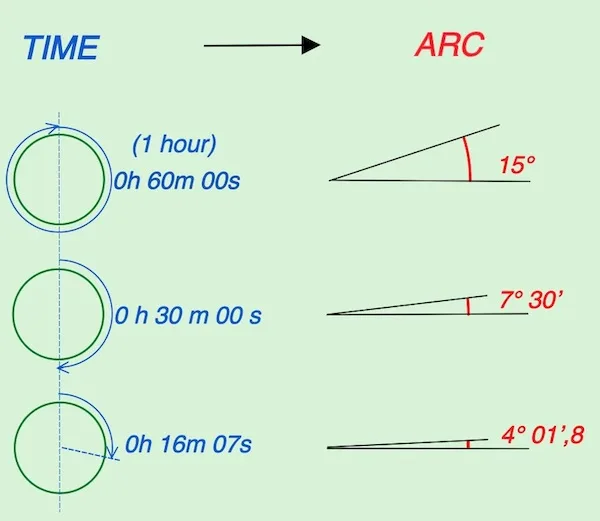
Increment of the sun’s hour angle
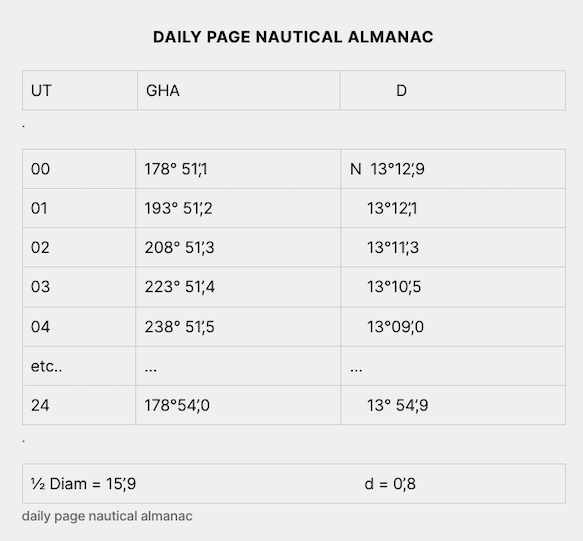
In conclusion we see in this daily page that the hour angle increases 15°00’,1 this day
(193°51’,2 – 178°51’,1 = 15° 00’,1) We neglect the 0’,1 for simplicity.
The Sun’s hour angle doesn’t precisely increase by 15 degrees every hour due to factors like the Earth’s elliptical orbit. This leads to a non-uniform rate of change in the Sun’s position in the sky throughout the year.
For practical purposes, we can use the increase in the Sun’s hour angle of exactly 15 degrees per hour for the calculation of time to arc.

example: time to arc
First, we start with the scientific calculator
For instance what is the the GHA at 02h 16m 07s UT ?

02 h 00m 00s UT ⇨ GHA = 208°51′,3
02 h 16m 07s UT ⇨ GHA = —-°—‘,-
03 h 00m 00s UT ⇨ GHA = 223°51′,4
In fact, (223°51’,4 – 208°51’,3 = 15° 00’,1) We neglect the 0’,1
As a result we start the increment calculation or pp (time to arc)
Whereas pp = proportional part of 15°
Next, use the scientific calculator method with the key [DMS] or [° ‘ “].

First, we consider 16 minutes et 07 secondes
Therefore, by inputting the given values of
0 h [° ‘ “],
16 m [° ‘ “],
07 s [° ‘ “]
into the scientific calculator using the [DMS] or [° ‘ “] key and multiplying the resulting angle in decimal form by 15, we arrive at the solution of 4.029167.
0 [° ‘ “] 16 [° ‘ “] 07[° ‘ “] x 15 = 4,029167,
Also don’t forget the first zero!
After obtaining the decimal answer, we convert it into degrees, minutes, and tenths of a minute using the inverse (DMS) button. (INV or SHIFT)
4,02967 [INV] [° ‘ “] ⇨ 4°01’ 45” ⇨ 4° 01′, 8
In conclusion, the sun’s hour angle has increased 4° 01′, 8 in 16minutes and 07 seconds
Note: We use a point (dot) — or sometimes a comma — to indicate tenths of a minute, as in 4°01′,8. This is standard in many nautical contexts and is equivalent to 4 degrees and 1.8 minutes.
How to round seconds in tenths of minutes:
60” = 1′ (60 seconds equal 1 minute)
| 10°10’ 06’’ | ⇨ 10°10’,1 |
| 10°10’ 12’’ | ⇨ 10°10’,2 |
| 10°10’ 18’’ | ⇨ 10°10’,3 |
| 10°10’ 24’’ | ⇨ 10°10’,4 |
| etc… | |
| 10°10’ 26, 28’’ | ⇨ 10°10’,4 |
| 10°10’ 27, 00’’ | ⇨ 10°10’,5 |
| 10°10’ 27, 31’’ | ⇨ 10°10’,5 |
| 10°10’ 30, 00’’ | ⇨ 10°10’,5 |
| etc… |
Even a small error of one-tenth of a minute is not critical.
Finally, calculate GHA at 02h 16m 07s UT
GHA = 208° 51’,3 (UT: 02h00m00s )
+incr. = 4° 01′, 8. (pp)
_______________
GHA = 212°53,1 (UT:02h 16m 07s)

Increment of the sun’s hour angle
exercises: time to arc


Increment and corrections tables
Second method time to arc: Instead of using a scientific calculator we use the permanent table of the nautical almanac
For instance we find for each minute a table with 60 seconds
Also see below that the pp (increment) for 16 minutes and 07 seconds
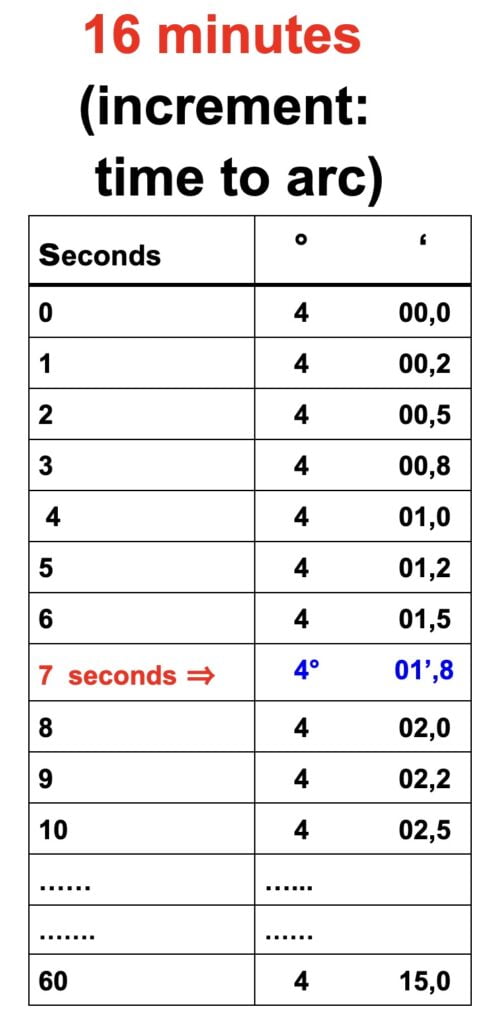
As a result pp = 4°01′, 8
21 pages for the increment tables
