EXPLANATION OF THE LOGARITHM TABLES
Introduction
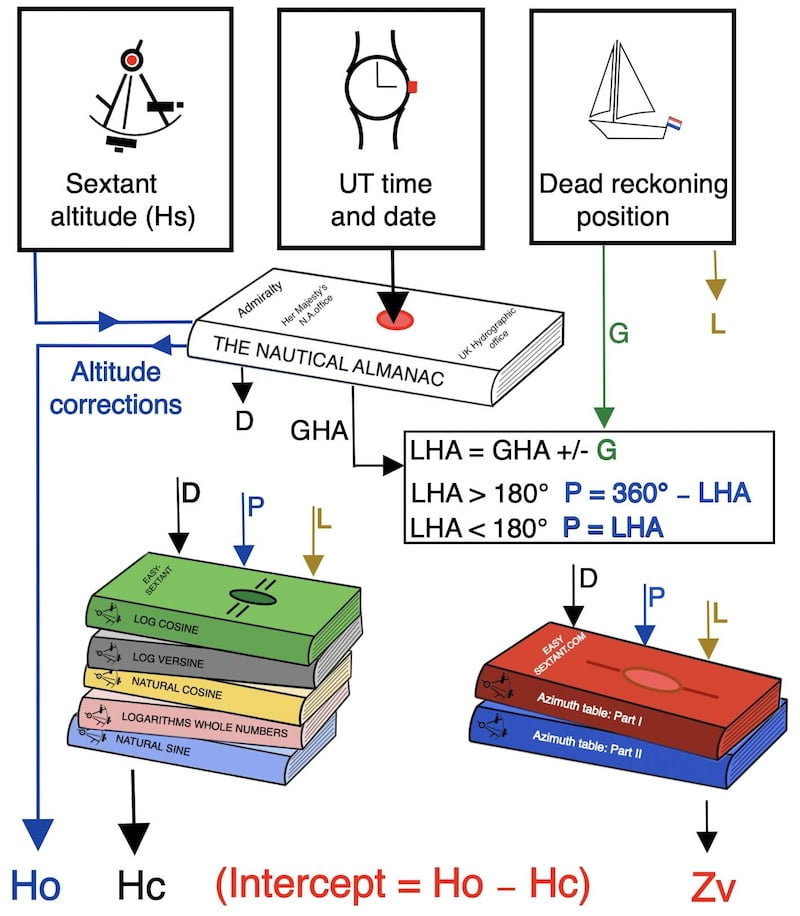
The celestial navigation method based on logarithms for calculating the Sun’s altitude was not invented by me; it was used for a very long time in the Dutch Navy. This traditional approach allows navigators to determine the Sun’s calculated altitude using only tables and a worksheet — no electronic devices required. This method originates from a logarithmic formula known as Douwes’ formula, after the Dutch mathematician and astronomer Dirk Douwes (1712–1773).
The five tables corresponding to this method were originally published together in one book (Zeevaartkundige Tafels — Nautical Tables), along with the worksheet itself. Of these, three are logarithmic. I have edited them separately to make them easier to use in chronological order and more readable — at the cost of a bit more paper and weight, though still quite reasonable.
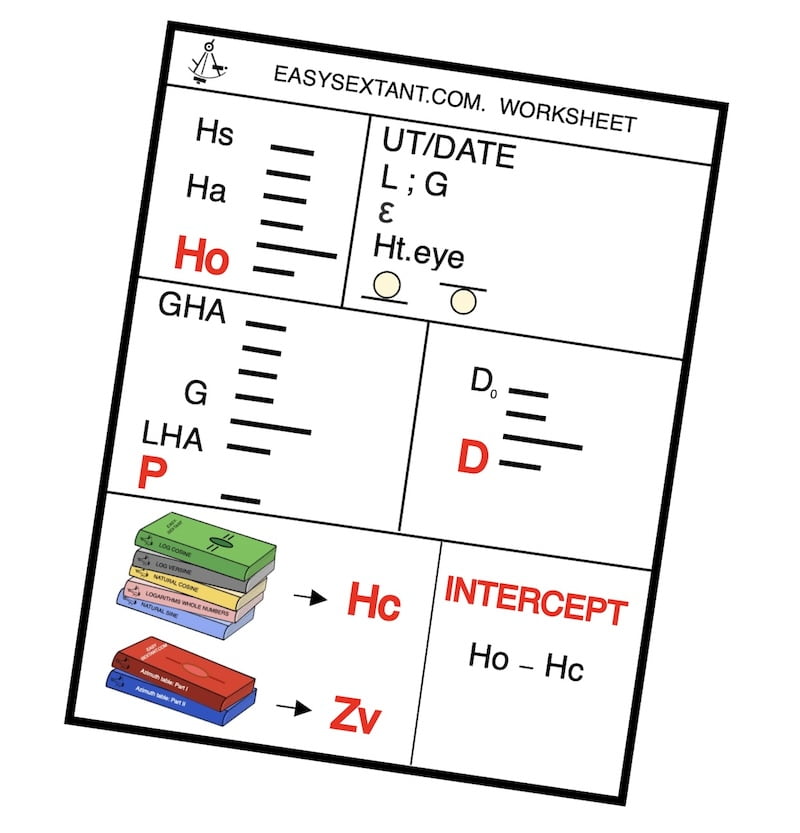
The essential point is to develop a mechanical way of working with these tables. Fill in the worksheet step by step, referring to the five tables in sequence, and perform the necessary additions and subtractions to obtain the calculated altitude. The worksheet grid and the five tables are available for free download on this page.
The key to understanding this logarithmic method is realizing that it replaces complex multiplications with simple additions. Mastery lies not in the theory of logarithms, but in mechanically filling in the grid and applying the rules of the five tables exactly as shown in this menu and its sub-menus.
First, please visit the Logarithm Main Page, which forms the basis of the “Logarithmic” menu and includes all the links that will guide you back to this page at the appropriate moment.
Logarithm tables: introduction and explanation
Firstly, these five tables should be used in order from 1 to 5 to gradually fill in the worksheet and obtain the calculated altitude of the sun.

Explanation of the logarithm tables.
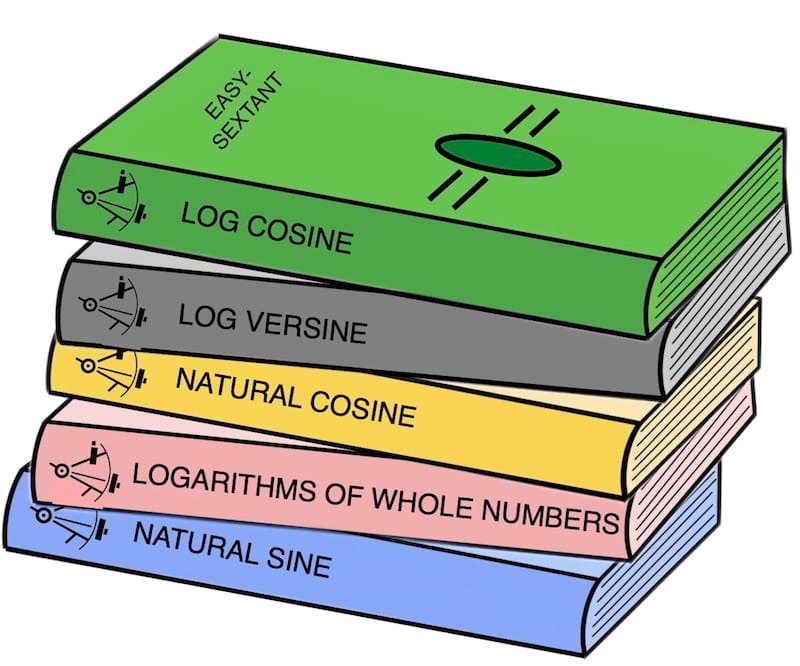

Table 1 to table 5:



For our purposes, logarithm tables replace multiplication with addition.
Additionally, we will find an example and two exercises completed below. (the necessary pages of the tables included).
The idea is to continue with the concept of the D.R. position, and intercept but we no longer use the rule of signs (positive or negative)
Consequently, we replace it with the concept of “same name” or “not same name.”

Method
The logarithm tables
Also, we adhere to the same Marcq Saint-Hilaire method.
Furthermore, do not confuse it with the American HO 249 tables for aviation, which are based on different methods and are less precise.
Hence, these logarithm tables do not depend on time either.
The five tables
The five tables necessary to obtain the calculated altitude (Hc)
- Table 1: log cosine
- Table 2: log versine
- Table 3: natural cosine
- Table 4: logarithms of whole numbers
- Table 5: natural sine


The author developed these tables with the help of Google Sheets.
The tables are relatively easy to use and should be arranged in order before beginning calculations on our worksheet.
I printed the logarithm tables along with the azimuth tables, using only one XL cartridge, or you can check with your local printing house.
Example of the five tables here:

Using Logarithm Tables with a Sextant at Sea:

To convert natural numbers to logarithmic values, you need to use Tables 1, and 2, then add these values together. Finally, Table 4 can be used to convert the logarithmic result back to a natural number.
Table 4 (logarithms of whole numbers)
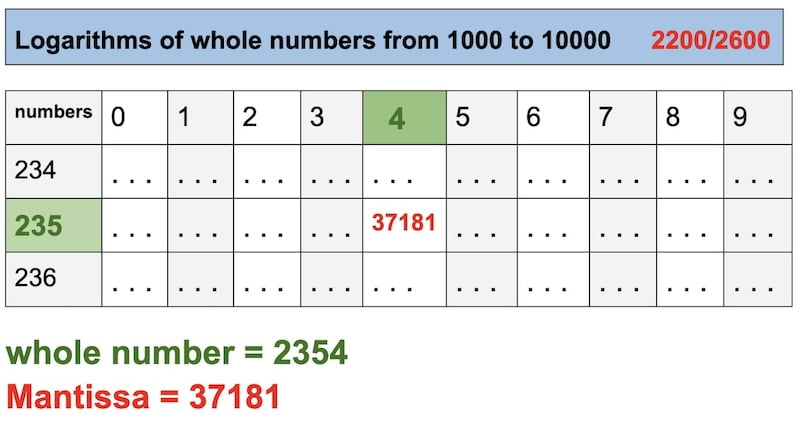
Table 4 is not intuitive at first, but it becomes easy to use once you know the rules.
In fact using tables as a tool, one does not need more knowledge in the sometimes very complicated world of logarithms.
Interpolation
It may happen that the input data into the table does not exactly match the values present in the table. In this case, it is necessary to use linear interpolation techniques between two values of the table.
You can estimate these interpolations and tolerate small errors (a few tenths of a minute of arc).
Use of tables
You can use these tables for the Sun, Moon, planets, and stars (up to 68° North or South in latitude and declination). They are not time-dependent.

Gain access to the exercises.
Indeed, in this course, you will find a total of four exercises with the logarithm tables, and the necessary pages of the tables and solution included.
Also, the interactive worksheet for the tables provides access to these four exercises on the following pages:
1) Example of calculating the Sun’s altitude (Hc) using logarithm tables.
2)Two exercises on calculating the Sun’s altitude (Hc) using logarithm tables, with solutions.
3) La Rochelle exercise option tables
Once you have gone through them and become familiar with them, you can test your skills on the seven remaining exercises in the exercise section..
You need to purchase the PDF answer files of the remaining exercises in the store.
This is an exceptional tool, but you need to be very organized!

For the purists, I explain how I established the worksheet using the Douwes formula, but you can directly go to the example of how to use the logarithm tables.
Douwes introduced the function Versine: (Versine is always positive) Explanation of the Douwes formula. Dutch mathematicians and astronomer (1712 – 1773)